题目内容


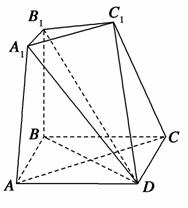
如图，在正三棱柱ABC－A1B1C1中，D是BC的中点，AA1＝AB＝a.

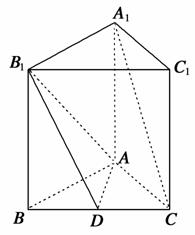
(1)求证：AD⊥B1D；

(2)求证：A1C∥平面AB1D；

(3)求三棱锥C－AB1D的体积．


[解析]　(1)证明：∵ABC－A1B1C1是正三棱柱，

∴BB1⊥平面ABC，

∵AD⊂平面ABC.∴AD⊥BB1.

又∵△ABC是正三角形，D是BC的中点，∴AD⊥BC.

又∵BC∩BB1＝B，

∴AD⊥平面B1BCC1.

又∵B1D⊂平面B1BCC1，

∴AD⊥B1D.

(2)证明：连接A1B，设A1B∩AB1＝E，连接DE.

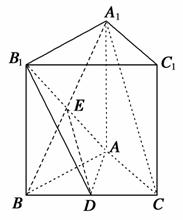
∵AA1＝AB，∴四边形A1ABB1是正方形，

∴E是A1B的中点，

又∵D是BC的中点，

∴DE∥A1C.

∵DE⊂平面AB1D，A1C⊄平面AB1D，

∴A1C∥平面AB1D.

(3)解：VC－AB1D＝VB1－ADC＝S△ADC·|BB1|＝a3.


练习册系列答案
相关题目

已知某几何体的俯视图是如图所示的边长为2的正方形，正视图与侧视图是边长为2的正三角形，则其表面积是(　　)

A．8                                                             B．12

C．4(1＋)                                               D．4

l1、l2、l3是空间三条不同的直线，则下列命题正确的是(　　)

A．l1⊥l2，l2⊥l3⇒l1∥l3

B．l1⊥l2，l2∥l3⇒l1⊥l3

C．l1∥l2∥l3⇒l1、l2、l3共面

D．l1、l2、l3共点⇒l1、l2、l3共面

已知m、n是两条直线，α、β是两个平面，给出下列命题：①若n⊥α，n⊥β，则α∥β；②若平面α上有不共线的三点到平面β的距离相等，则α∥β；③若n、m为异面直线，n⊂α，n∥β，m⊂β，m∥α，则α∥β.其中正确命题的个数是(　　)

A．3个　　　                                                B．2个　　　

C．1个　　　                                                D．0个

已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列命题：

①若m∥α，n∥α，m∥β，n∥β，则α∥β；

②若α⊥γ，β⊥γ，α∩β＝m，n⊂γ，则m⊥n；

③若m⊥α，α⊥β，m∥n，则n∥β；

④若n∥α，n∥β，α∩β＝m，那么m∥n.

其中正确命题的序号是________．

设两个平面α、β，直线l，下列三个条件：①l⊥α；②l∥β；③α⊥β.若以其中两个作为前提，另一个作为结论，则可构成三个命题，这三个命题中正确命题的个数为(　　)

A．3　　 　　                                               B．2　　 　　

C．1　　 　　                                               D．0

在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，下面四个结论中不成立的是(　　)

A．BC∥平面PDF                                        B．DF⊥平面PAE

C．平面PDF⊥平面ABC                              D．平面PAE⊥平面ABC

 如图所示的七面体是由三棱台ABC－A1B1C1和四棱锥D－AA1C1C对接而成，四边形ABCD是边长为2的正方形，BB1⊥平面ABCD，BB1＝2A1B1＝2.

(1)求证：平面AA1C1C⊥平面BB1D；

(2)求二面角A－A1D－C1的余弦值．

如图是某个正方体的侧面展开图，l1，l2是两条侧面对角线，则在正方体中，l1与l2(　　)

A．互相平行

B．异面且互相垂直

C．异面且夹角为

D．相交且夹角为

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网