题目内容
如图,在四棱锥P-ABCD中,ABCD为平行四边形,且BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.
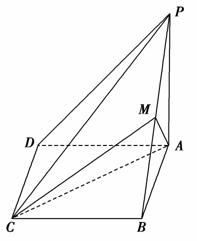
(1)求证:PD∥平面AMC;
(2)求三棱锥A-MBC的高.
[解析]
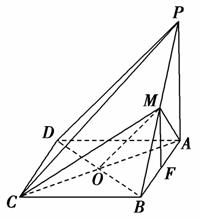
(1)如图,连接BD,设BD与AC相交于点O,连接OM,
∵四边形ABCD是平行四边形,
∴点O为BD的中点.
∵M为PB的中点,
∴OM为△PBD的中位线,
∴OM∥PD,
∵OM⊂平面AMC,PD⊄平面AMC,
∴PD∥平面AMC.
(2)∵BC⊥平面PAB,AD∥BC,
∴AD⊥平面PAB,∴PA⊥AD,
又PA⊥AB,且AD∩AB=A,
∴PA⊥平面ABCD.
取AB的中点F,连接MF,则MF∥PA,
∴MF⊥平面ABCD,且MF=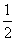 PA=1.
PA=1.
设三棱锥A-MBC的高为h,
由VA-MBC=VM-ABC,得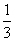 S△MBC·h=
S△MBC·h=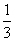 S△ABC·MF,
S△ABC·MF,
得h=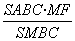 =
=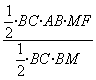 =
=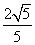 .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 B.
B.
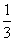 D.
D.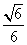
 ,若球O的体积为
,若球O的体积为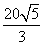 π,则这个直三棱柱的体积等于( )
π,则这个直三棱柱的体积等于( )
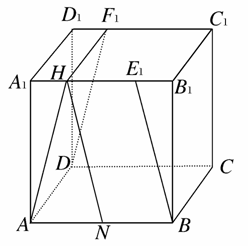
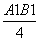 ,求BE1与DF1所成角的余弦值.
,求BE1与DF1所成角的余弦值.