题目内容
某商场组织有奖竞猜活动，参与者需要先后回答两道选择题，问题A有三个选项，问题B有四个选项，但都只有一个选项是正确的，正确回答问题A可获奖金25元，正确回答问题B可获奖金30元，活动规定：参与者可任意选择回答问题的顺序，如果第一个问题回答正确，则继续答题，否则该参与者猜奖活动终止，假设一个参与者在回答问题前，对这两个问题都很陌生，只能用蒙猜的办法答题．
（1）如果参与者先回答问题A，求其获得奖金25元的概率；
（2）试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大．
（1）如果参与者先回答问题A，求其获得奖金25元的概率；
（2）试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大．
考点：离散型随机变量及其分布列
专题：概率与统计
分析：（1）随机猜对问题A的概率P1=
，随机猜对问题B的概率P2=
．由此能求出参与者先回答问题A，且获得奖金25元概率．
（2）参与者回答问题的顺序有两种，分别讨论如下：①先回答问题A再回答问题B，参与者获奖金额ξ可取0，25，55，②先回答问题B再回答问题A，参与者获奖金额η可取0，30，55．分别求出相应的期望能得到应该先答问题A，再答问题B能使该参与者获奖金额的期望值较大．
| 1 |
| 3 |
| 1 |
| 4 |
（2）参与者回答问题的顺序有两种，分别讨论如下：①先回答问题A再回答问题B，参与者获奖金额ξ可取0，25，55，②先回答问题B再回答问题A，参与者获奖金额η可取0，30，55．分别求出相应的期望能得到应该先答问题A，再答问题B能使该参与者获奖金额的期望值较大．
解答：
解：（1）随机猜对问题A的概率P1=
，
随机猜对问题B的概率P2=
．
设参与者先回答问题A，且获得奖金25元为事件M，
则P(M)=P1(1-P2)=
×
=
，
即参与者先回答问题A，且获得奖金25元概率为
．（5分）
（2）参与者回答问题的顺序有两种，分别讨论如下：
①先回答问题A再回答问题B，参与者获奖金额ξ可取0，25，55，
则P(ξ=0)=1-P1=
，
P(ξ=25)=P1(1-P2)=
，
P(ξ=55)=P1P2=
（8分）
E(ξ)=
．
②先回答问题B再回答问题A，参与者获奖金额η可取0，30，55
则P(η=0)=1-P2=
，
P(η=30)=P2(1-P1)=
，
P(η=55)=P1P2=
，
E(η)=
．
因为E（ξ）＞E（η），所以应该先答问题A，再答问题B．（12分）
| 1 |
| 3 |
随机猜对问题B的概率P2=
| 1 |
| 4 |
设参与者先回答问题A，且获得奖金25元为事件M，
则P(M)=P1(1-P2)=
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
即参与者先回答问题A，且获得奖金25元概率为
| 1 |
| 4 |
（2）参与者回答问题的顺序有两种，分别讨论如下：
①先回答问题A再回答问题B，参与者获奖金额ξ可取0，25，55，
则P(ξ=0)=1-P1=
| 2 |
| 3 |
P(ξ=25)=P1(1-P2)=
| 1 |
| 4 |
P(ξ=55)=P1P2=
| 1 |
| 12 |
E(ξ)=
| 130 |
| 12 |
②先回答问题B再回答问题A，参与者获奖金额η可取0，30，55
则P(η=0)=1-P2=
| 3 |
| 4 |
P(η=30)=P2(1-P1)=
| 1 |
| 6 |
P(η=55)=P1P2=
| 1 |
| 12 |
E(η)=
| 115 |
| 12 |
因为E（ξ）＞E（η），所以应该先答问题A，再答问题B．（12分）
点评：本题考查概率的求法，考查离散型随机变量的期望的求法，是中档题，在历年高考中都是必考题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
方程x2+y2+2ax+2by+a2+b2=0表示的图形是（ ）
| A、以（a，b）为圆心的圆 |
| B、以（-a，-b）为圆心的圆 |
| C、点（a，b） |
| D、点（-a，-b） |
如图所示，网格纸上小正方形的边长为1cm，粗实线为某空间几何体的三视图，则该几何体的体积为（ ）
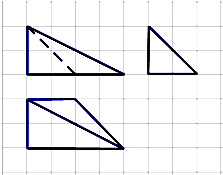
| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
设m、n是两条不同的直线，α、β是两个不同的平面，下列命题中错误的是（ ）
| A、若m⊥α，m∥n，n∥β，则α⊥β |
| B、若α⊥β，m?α，m⊥β，则m∥α |
| C、若m⊥β，m?α，则α⊥β |
| D、若α⊥β，m?α，n?β，则m⊥n |
函数f（x）=
的定义域为（ ）
| lg(x2-1) | ||
|
| A、（-∞，-2）∪（1，+∞） |
| B、（-2，1） |
| C、（-∞，-1）∪（2，+∞） |
| D、（1，2） |