题目内容
13.已知二次函数g(x)=-2x2+6x-1,则:(1)其对称轴:$\frac{3}{2}$;
(2)顶点坐标为($\frac{3}{2}$,$\frac{7}{2}$);
(3)单调区间为(-∞,$\frac{3}{2}$)和($\frac{3}{2}$,+∞);
(4)g(x)的最大值为$\frac{7}{2}$.
分析 根据二次函数的性质分别求出即可.
解答 解:已知二次函数g(x)=-2x2+6x-1,则:
(1)其对称轴:x=-$\frac{6}{2×(-2)}$=$\frac{3}{2}$;
(2)g(x)=-2x2+6x-1=-2${(x-\frac{3}{2})}^{2}$+$\frac{7}{2}$,顶点坐标为 ($\frac{3}{2}$,$\frac{7}{2}$);
(3)g(x)在(-∞,$\frac{3}{2}$)递增,在($\frac{3}{2}$,+∞)递递减;
(4)g(x)的最大值是g($\frac{3}{2}$)=$\frac{7}{2}$;
故答案为:$\frac{3}{2}$; ($\frac{3}{2}$,$\frac{7}{2}$);(-∞,$\frac{3}{2}$),($\frac{3}{2}$,+∞);$\frac{7}{2}$.
点评 本题考察了二次函数的性质,是一道基础题.

练习册系列答案
相关题目
1.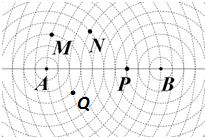 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )| A. | eM<eN<eQ<eP | B. | eN<eM<eP<eQ | C. | eP<eQ<eM<eN | D. | eQ<eN<eM<eP |
18.用与球心距离为4的平面去截球所得的截面面积为9π,则球的表面积为( )
| A. | 36π | B. | 64π | C. | 100π | D. | 144π |