��Ŀ����
1��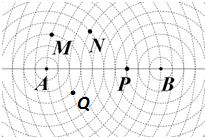 ��ͼ����֪|AB|=10��ͼ�е�һϵ��Բ��Բ�ķֱ�ΪA��B������ͬ��Բ��ÿ��ͬ��Բ�İ뾶�ֱ���1��2��3������n����������������ͬ��Բ���Ի�����A��BΪ�������Բ��˫���ߣ������о�����M��N����Բ�������ʷֱ���eM��eN��������P��Q��˫���ߵ������ʷֱ���eP��eQ�������ǵĴ�С��ϵ�ǣ�������
��ͼ����֪|AB|=10��ͼ�е�һϵ��Բ��Բ�ķֱ�ΪA��B������ͬ��Բ��ÿ��ͬ��Բ�İ뾶�ֱ���1��2��3������n����������������ͬ��Բ���Ի�����A��BΪ�������Բ��˫���ߣ������о�����M��N����Բ�������ʷֱ���eM��eN��������P��Q��˫���ߵ������ʷֱ���eP��eQ�������ǵĴ�С��ϵ�ǣ�������| A�� | eM��eN��eQ��eP | B�� | eN��eM��eP��eQ | C�� | eP��eQ��eM��eN | D�� | eQ��eN��eM��eP |
���� �������֪�����е�˫���ߵĽ���һ��Ϊ|AB|=10����2c=10��c=5������Բ�Ķ���ֱ����eM��eN����˫���ߵĶ��壬�ֱ����eP��eQ���ɴ��ܱȽ�eM��eN��eP��eQ�Ĵ�С��ϵ��
��� �⣺�������֪�����е�˫���ߵĽ���һ��Ϊ|AB|=10����2c=10��c=5��
����Բ�Ķ��壺
�Թ�M�����Բ��|PA|+|PB|=2a=3+10=13��
��a=$\frac{13}{2}$��${e}_{M}=\frac{5}{\frac{13}{2}}$=$\frac{10}{13}$��
�Թ�N�����Բ��|PA|+|PB|=2a=5+7=12��
��a=6��${e}_{N}=\frac{5}{6}$��
��˫���ߵĶ��壺
�Թ�P���˫���ߣ�||PA|-|PB||=2a=|7-3|=4��
��a=2��eP=$\frac{5}{2}$��
�Թ�Q���˫���ߣ�||PA|-|PB||=2a=|3-8|=5��
��a=$\frac{5}{2}$��${e}_{Q}=\frac{5}{\frac{5}{2}}$=2��
��eM��eN��eQ��eP��
��ѡ��A��
���� ���⿼��˫���ߺ���Բ�������ʵĴ�С��ϵ�ıȽϣ��ǻ����⣬����ʱҪ�������⣬ע����Բ��˫���ߵ����ʵĺ������ã�

��ϰ��ϵ�д�
 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
�����Ŀ
11���ڡ�ABC�У�$a=3��c=2��B=\frac{��}{3}$����b=��������
| A�� | 19 | B�� | 7 | C�� | $\sqrt{19}$ | D�� | $\sqrt{7}$ |
12����֪A��B��C��D������O�������ϣ�AB=BC=1��AC=$\sqrt{3}$��������D-ABC��������ֵ��$\frac{1}{4}$������O�ı����Ϊ��������
| A�� | $\frac{4}{3}$�� | B�� | $\frac{8}{3}$�� | C�� | $\frac{16}{3}$�� | D�� | 6�� |
9����֪�Ȳ�����{an}�У�a1+a3=16����a2=��������
| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 10 |
6����֪����p��?x��R��2x��3x������q������y=2x2-7����P��3��9��������б��Ϊ12��������������Ϊ��������ǣ�������
| A�� | p��q | B�� | �Vp��q | C�� | p�ĩVq | D�� | �Vp�ĩVq |