题目内容
某工厂的一个车间有5台同一型号机器均在独立运行,一天中每台机器发生故障的概率为0.1,若每一天该车间获取利润y(万元)与“不发生故障”的机器台数n(n∈N,n≤5)之间满足关系式:y=
(Ⅰ)求某一天中有两台机器发生故障的概率;
(Ⅱ)求这个车间一天内可能获取利润的均值(.精确到0.01).
|
(Ⅰ)求某一天中有两台机器发生故障的概率;
(Ⅱ)求这个车间一天内可能获取利润的均值(.精确到0.01).
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(Ⅰ)利用相互独立事件的概率公式,求某一天中有两台机器发生故障的概率;
(Ⅱ)利用每一天该车间获取利润y(万元)与“不发生故障”的机器台数n(n∈N,n≤5)之间满足关系式:y=
,结合相互独立事件的概率公式,求这个车间一天内可能获取利润的均值.
(Ⅱ)利用每一天该车间获取利润y(万元)与“不发生故障”的机器台数n(n∈N,n≤5)之间满足关系式:y=
|
解答:
解:(Ⅰ)∵一天中每台机器发生故障的概率为0.1,
∴某一天中有两台机器发生故障的概率为
•0.12•0.93=0.0729;
(Ⅱ)∵每一天该车间获取利润y(万元)与“不发生故障”的机器台数n(n∈N,n≤5)之间满足关系式:y=
又P0=
•0.95=0.95,P1=
•0.1•0.94=0.5•0.94,
∴这个车间一天内可能获取利润的均值P0•12+P1•9+P2•6+(P3+P4+P5)•(-6)
=P0•12+P1•9+P2•6+(1-P0-P1-P2)•(-6)=18P0+15P1+12P2-6≈10.42万元.
∴某一天中有两台机器发生故障的概率为
| C | 2 5 |
(Ⅱ)∵每一天该车间获取利润y(万元)与“不发生故障”的机器台数n(n∈N,n≤5)之间满足关系式:y=
|
又P0=
| C | 0 5 |
| C | 1 5 |
∴这个车间一天内可能获取利润的均值P0•12+P1•9+P2•6+(P3+P4+P5)•(-6)
=P0•12+P1•9+P2•6+(1-P0-P1-P2)•(-6)=18P0+15P1+12P2-6≈10.42万元.
点评:本题考查函数模型的选择与应用,考查相互独立事件的概率公式,正确运用相互独立事件的概率公式,是关键.

练习册系列答案
相关题目
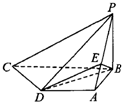 如图所示,四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA,则平面ABE与平面BED的夹角的余弦值为
如图所示,四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA,则平面ABE与平面BED的夹角的余弦值为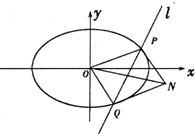 已知椭圆C:
已知椭圆C: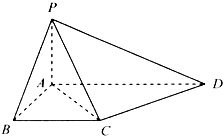 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=