题目内容
函数f（x）=3x-x3+4在x∈[1，2]的最大值和最小值．
考点：利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：根据导数判断出函数为单调增函数，继而求出最值．
解答：
解：∵函数f（x）=3x-x3+4，
f′（x）=-3x2+3=-3（x2-1）．
令x2-1=0，解得x=1或x=-1，
∴函数f（x）=3x-x3+4在x∈[1，2]的最大值和最小值，在端点处取得，
∴f（x）min=f（2）=6-8+4=2，f（x）max=f（1）=3-1+4=6．
函数f（x）=3x-x3+4在x∈[1，2]的最大值和最小值分别为：6；2．
f′（x）=-3x2+3=-3（x2-1）．
令x2-1=0，解得x=1或x=-1，
∴函数f（x）=3x-x3+4在x∈[1，2]的最大值和最小值，在端点处取得，
∴f（x）min=f（2）=6-8+4=2，f（x）max=f（1）=3-1+4=6．
函数f（x）=3x-x3+4在x∈[1，2]的最大值和最小值分别为：6；2．
点评：本题考查了用导数求闭区间上函数的最值的问题，属于基础题．
练习册系列答案
相关题目
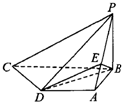如图所示，四棱锥P-ABCD中，PB⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA，则平面ABE与平面BED的夹角的余弦值为
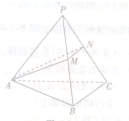如图所示，在三棱锥P-ABC中，PA=PB=PC，底面△ABC是正三角形，M、N分别是侧棱PB、PC的中点，若平面AMN⊥平面PBC，则平面AMN与平面ABC成二面角（锐角）的余弦值等于（ ）