题目内容
18.已知(a+x)(1-x)6的展开式中x3的系数为5,则实数a=$\frac{1}{2}$.分析 (1-x)6的展开式的通项公式Tr+1=${∁}_{6}^{r}$(-x)r,分别令r=2,3,可得:(a+x)(1-x)6的展开式中x3的系数为:${∁}_{6}^{2}(-1)^{2}$+a$•{∁}_{6}^{3}$(-1)3.即可得出.
解答 解:(1-x)6的展开式的通项公式Tr+1=${∁}_{6}^{r}$(-x)r,
分别令r=2,3,可得:(a+x)(1-x)6的展开式中x3的系数为:${∁}_{6}^{2}(-1)^{2}$+a$•{∁}_{6}^{3}$(-1)3.
∴${∁}_{6}^{2}(-1)^{2}$+a$•{∁}_{6}^{3}$(-1)3=5.
化为15-20a=5,
解得a=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若集合$M=\left\{{x∈R\left|{\frac{x+2}{x-1}≤0}\right.}\right\}{,_{\;}}N$为自然数集,则下列选项正确的是( )
| A. | M⊆{x|x≥1} | B. | M⊆{x|x>-2} | C. | M∩N={0} | D. | M∪N=N |
7.已知数列{an}满足an+1+an=n,若a1=2,则a8-a4=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |

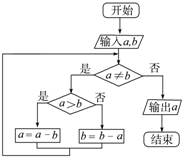 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,20,则输出的a=2.
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,20,则输出的a=2.