题目内容
2. 如图几何体中,长方形ACDF所在平面与梯形BCDE所在平面垂直,且BC=2DE,DE∥BC,BD⊥AD,M为AB的中点..
如图几何体中,长方形ACDF所在平面与梯形BCDE所在平面垂直,且BC=2DE,DE∥BC,BD⊥AD,M为AB的中点..(Ⅰ)证明:EM∥平面ACDF;
(Ⅱ)证明:BD⊥平面ACDF.
分析 (Ⅰ)取BC中点N,连结EN、MN,推导出平面EMN∥平面ACDF,由此能证明EM∥平面ACDF.
(2)由已知AC⊥平面BCDE,从而AC⊥BD,再由BD⊥AD,AC∩AD=A,能证明BD⊥平面ACDF.
解答 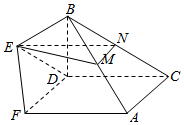 证明:(Ⅰ)取BC中点N,连结EN、MN,
证明:(Ⅰ)取BC中点N,连结EN、MN,
∵长方形ACDF所在平面与梯形BCDE所在平面垂直,且BC=2DE,DE∥BC,BD⊥AD,M为AB的中点,
∴EN∥CD,MN∥AC,
∵EN∩MN=N,CD∩AC=C,
EN,MN?平面EMN,CD,AC?平面ACDF,
∴平面EMN∥平面ACDF,
∵EM?平面EMN,∴EM∥平面ACDF.
(2)∵长方形ACDF中,AC⊥CD,长方形ACDF所在平面与梯形BCDE所在平面垂直,
∴AC⊥平面BCDE,
∵BD?平面BCDE,∴AC⊥BD,
∵BD⊥AD,AC∩AD=A,
∴BD⊥平面ACDF.
点评 本题考查线面平行、线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
12.在△ABC中,若$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),则下列关系式正确的是( )
| A. | BD=2CD | B. | BD=CD | C. | BD=3CD | D. | CD=2BD |
13.函数$f(x)=\frac{1}{x}+{log_{\frac{1}{2}}}x$的零点位于区间( )
| A. | $({\frac{1}{4},\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (1,2) | D. | (2,4) |
10.已知数列{an}是正项等比数列,满足an+2=2an+1+3an,且首项为方程x2+2x-3=0的一个根.则下列等式成立的是( )
| A. | an+1=2Sn+1 | B. | an=2Sn+1 | C. | an+1=Sn+1 | D. | an=2Sn-1-1 |
17.已知A={1,2,4,8,16},B={y|y=log2x,x∈A},则A∩B=( )
| A. | {1,2} | B. | {2,4,8} | C. | {1,2,4} | D. | {1,2,4,8} |
7.已知函数f(x)=$\left\{\begin{array}{l}{x^4}+1,x>0\\ cos2x,x≤0\end{array}\right.$,则下列结论正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是增函数 | C. | f(x)是周期函数 | D. | f(x)的值域为[-1,+∞) |
14.将2名女教师,4名男教师分成2个小组,分别安排到甲、乙两所学校轮岗支教,每个小组由1名女教师和2名男教师组成,则不同的安排方案共有( )
| A. | 24种 | B. | 12种 | C. | 10种 | D. | 9种 |
 已知直线l:x=5,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,A是椭圆C上任意一点,|AF|的最小值为$\sqrt{5}$-1,且点A到直线l的距离最小值为5-$\sqrt{5}$.
已知直线l:x=5,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,A是椭圆C上任意一点,|AF|的最小值为$\sqrt{5}$-1,且点A到直线l的距离最小值为5-$\sqrt{5}$.