将2名女教师.4名男教师分成2个小组.分别安排到甲.乙两所学校轮岗支教.每个小组由1名女教师和2名男教师组成.则不同的安排方案共有( )A．24种B．12种C．10种D．9种题目和参考答案——青夏教育精英家教网—

题目内容

14．将2名女教师，4名男教师分成2个小组，分别安排到甲、乙两所学校轮岗支教，每个小组由1名女教师和2名男教师组成，则不同的安排方案共有（　　）

A．

24种

B．

12种

C．

10种

D．

9种

分析将任务分三步完成，在每步中利用排列和组合的方法计数，最后利用分步计数原理，将各步结果相乘即可得结果

解答解：第一步，为甲地选一女老师，有C₂¹=2种选法；
第二步，为甲地选两个男教师，有C₄²=6种选法；
第三步，剩下的三名教师到乙地，
故不同的安排方案共有2×6×1=12种，
故选B．

点评本题主要考查了分步计数原理的应用，排列组合计数的方法，理解题意，恰当分步是解决本题的关键，属基础题

练习册系列答案

5．已知平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$，|$\overrightarrow{a}$|=$\sqrt{3}$，|$\overrightarrow{b}$|=1，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=1．

2．

如图几何体中，长方形ACDF所在平面与梯形BCDE所在平面垂直，且BC=2DE，DE∥BC，BD⊥AD，M为AB的中点．．
（Ⅰ）证明：EM∥平面ACDF；
（Ⅱ）证明：BD⊥平面ACDF．

9．（x-2y）⁶的展开式中，x⁴y²的系数为（　　）

19．函数f（x）=$\sqrt{2-{2}^{x}}$+$\frac{1}{lo{g}_{3}x}$的定义域为（　　）

6．

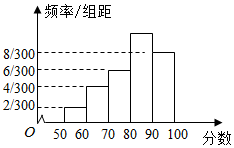某校为了解一个英语教改实验班的情况，举行了一次测试，将该班30位学生的英语成绩进行统计，得图示频率分布直方图，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求出该班学生英语成绩的众数和平均数；
（2）从成绩低于80分得学生中随机抽取2人，规定抽到的学生成绩在[50，60）的记1绩点分，在[60，80）的记2绩点分，设抽取2人的总绩点分为ξ，求ξ的分布列和数学期望．

3．函数f（x）=sinx（sinx+$\sqrt{3}$cosx）的最大值为（　　）

4．已知数列{a_n}前n项和S_n，${a_n}=1-2{S_n}_{\;}（{n∈{N^*}}）$．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若${b_n}={log_{\frac{1}{3}}}{a_{2n-1}}，{c_n}=\frac{{4{n^2}}}{{{b_n}{b_{n+1}}}}，{T_n}$为数列{c_n}的前n项和，求不超过T₂₀₁₆的最大的整数k．

试题分类