题目内容

14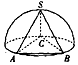．如图，已知底面为正三角形，侧棱长都相等的三棱锥S-ABC各顶点都在半球面上，其中A、B、C三顶点在底面圆周上，若三棱锥S-ABC的体积为2$\sqrt{3}$，则该半球的体积为$\frac{16π}{3}$．

分析 设球的半径为R，则AB=$\sqrt{3}R$，由三棱锥S-ABC的体积为2$\sqrt{3}$，求出R=2，由此能求出该半球的体积．

解答 解：设球的半径为R，
∵底面为正三角形，侧棱长都相等的三棱锥S-ABC各顶点都在半球面上，
其中A、B、C三顶点在底面圆周上，
∴AB=$\sqrt{3}R$，
∵三棱锥S-ABC的体积为2$\sqrt{3}$，
∴VS-ABC=$\frac{1}{3}×\frac{\sqrt{3}}{4}×（\sqrt{3}R）^{3}$=2$\sqrt{3}$，
解得R=2，
∴该半球的体积为V=$\frac{1}{2}×\frac{4}{3}π×{2}^{3}$=$\frac{16π}{3}$．
故答案为：$\frac{16π}{3}$．

点评 本题主要考查球、三棱锥的概念和性质，圆的性质等知识，意在考查转化和化归思想，数形结合思想和学生的运算求解能力，是中档题．

练习册系列答案
相关题目
4．已知椭圆$M：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率是$\frac{{\sqrt{2}}}{2}$，上顶点B是抛物线x2=4y的焦点．
（1）求椭圆M的标准方程；
（2）若P、Q是椭圆M上的两个动点，且OP⊥OQ（O是坐标原点），试问：点到直线的距离是否为定值？若是，试求出这个定值；若不是，请说明理由．
5．向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（2，1），则（$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{b}$-2$\overrightarrow{a}$）=（　　）
A．-2B．-1C．1D．0
2．若求O的半径为4，且球心O到平面α的距离为$\sqrt{3}$，则平面α截球O所得截面圆的面积为（　　）
A．πB．10πC．13πD．52π
9．定义在R上的奇函数f（x）满足f（2+x）=f（2-x），当x∈[0，2）时，f（x）=-4x2+8x．若在区间[a，b]上，存在m（m≥3）个不同的整数x（i=1，2，…，m），满足$\sum_{i=1}^{m=1}{|{f（x）-f（{x_{i+1}}）}|}≥72$，则b-a的最小值为（　　）
A．15B．16C．17D．18
19．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左右焦点与其短轴的一个端点是正三角形的三个顶点，点D$（{1，\frac{3}{2}}）$在椭圆C上，直线l：y=kx+m与椭圆C相交于A、P两点，与x轴、y轴分别相交于点N和M，且PM=MN，点Q是点P关于x轴的对称点，QM的延长线交椭圆于点B，过点A、B分别作x轴的垂涎，垂足分别为A1、B1
（1）求椭圆C的方程；
（2）是否存在直线l，使得点N平分线段A1B1？若存在，求求出直线l的方程，若不存在，请说明理由．
6．已知E（1，0），K（-1，0），P是平面上一动点，且满足$|\overrightarrow{PE}|•|\overrightarrow{KE}|=\overrightarrow{PK}•\overrightarrow{EK}$．
（1）求点P的轨迹C对应的方程；
（2）过点K的直线l与C相交于A、B两点（A点在x轴上方），点A关于x轴的对称点为D，且$\overrightarrow{EA}•\overrightarrow{EB}=-8$，求△ABD的外接圆的方程．
3．事件A，B是相互独立的，P（A）=0.4，P（B）=0.3，下列四个式子：①P（AB）=0.12；②P（$\overline{A}$B）=0.18；③P（A$\overline{B}$）=0.28；④P（$\overline{A}$$\overline{B}$）=0.42．其中正确的有（　　）
A．4个B．2个C．3个D．1个
4．已知函数f（x）=sin（x-$\frac{π}{6}$）cosx+1．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）当x∈[$\frac{π}{12}$，$\frac{π}{2}$]时，求函数f（x）的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网