题目内容
5．向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（2，1），则（$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{b}$-2$\overrightarrow{a}$）=（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 0 |
分析 根据平面向量的坐标运算与数量积运算，计算即可．
解答 解：向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（2，1），
则$\overrightarrow{a}$+$\overrightarrow{b}$=（3，1），
$\overrightarrow{b}$-2$\overrightarrow{a}$=（0，1），
所以（$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{b}$-2$\overrightarrow{a}$）=3×0+1×1=1．
故选：C．
点评 本题考查了平面向量的坐标运算与数量积运算问题，是基础题．
练习册系列答案
相关题目
15．下列命题中，真命题是（ ）
| A． | 存在x∈R，ex≤0 | B． | a+b=0的充要条件是$\frac{a}{b}$=-1 | ||
| C． | 任意x∈R，2x＞x2 | D． | a＞1，b＞1是ab＞1的充分条件 |
16．已知x2+y 2=1，若x+y-k≥0对符合条件一切x、y都成立，则实数k的最大值为（ ）
| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | 0 | D． | 1 |
20．已知角a的终边经过点P（-4，m），且$sinα=\frac{3}{5}$，则m等于（ ）
| A． | 3 | B． | $\frac{3}{5}$ | C． | -3 | D． | $-\frac{3}{5}$ |
10．为了了解高血压是否与常喝酒有关，现对30名成年人进行了问卷调查得到如下列联表：
已知在全部30人中随机抽取1人，抽到正常血压成年人的概率为$\frac{2}{5}$．
（1）请将上面的列联表补充完整；
（2）是否有99%的把握认为高血压与常喝酒有关？说明理由；
（3）4名调查人员随机分成两组，每组2人，一组负责问卷调查，另一组负责数据处理，求工作人员甲分到负责收集数据组，工作人员乙分到负责数据处理组的概率．
参考数据：
（参考公式：K2=$\frac{{n（ad-bc）}^{2}}{（a+b）（c+d）（a+c）（b+d）}$）
| 常喝 | 不常喝 | 合计 | |
| 正常血压 | 4 | 8 | 12 |
| 高血压 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
（1）请将上面的列联表补充完整；
（2）是否有99%的把握认为高血压与常喝酒有关？说明理由；
（3）4名调查人员随机分成两组，每组2人，一组负责问卷调查，另一组负责数据处理，求工作人员甲分到负责收集数据组，工作人员乙分到负责数据处理组的概率．
参考数据：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17．函数$y=sin\frac{1}{2}x$（ ）
| A． | 在[-π，π]上是增函数 | B． | 在[0，π]上是减函数 | ||
| C． | 在$[{-\frac{π}{2}，\frac{π}{2}}]$上是减函数 | D． | 在[-π，0]上是减函数 |
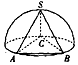如图，已知底面为正三角形，侧棱长都相等的三棱锥S-ABC各顶点都在半球面上，其中A、B、C三顶点在底面圆周上，若三棱锥S-ABC的体积为2$\sqrt{3}$，则该半球的体积为$\frac{16π}{3}$．