题目内容
3.事件A,B是相互独立的,P(A)=0.4,P(B)=0.3,下列四个式子:①P(AB)=0.12;②P($\overline{A}$B)=0.18;③P(A$\overline{B}$)=0.28;④P($\overline{A}$$\overline{B}$)=0.42.其中正确的有( )| A. | 4个 | B. | 2个 | C. | 3个 | D. | 1个 |
分析 利用相互独立事件概率乘法公式和对立事件概率计算公式求解.
解答 解:事件A,B是相互独立的,P(A)=0.4,P(B)=0.3,知:
在①中,P(AB)=P(A)P(B)=0.4×0.3=0.12,故①正确;
在②中,P($\overline{A}$B)=P($\overline{A}$)P(B)=0.6×0.3=0.18,故②正确;
在③中,P(A$\overline{B}$)=P(A)P($\overline{B}$)=0.4×0.7=0.28,故③正确;
在④中,P($\overline{A}$$\overline{B}$)=P($\overline{A}$)P($\overline{B}$)=0.6×0.7=0.42,故④正确.
故选:A.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式和对立事件概率计算公式的合理运用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
12.某学校为了制定治理学校门口上学,放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,得到了如下的列联表(单位:人)
已知在抽取的50分调查问卷中速记抽取一份,抽到不同意限定区域停车问卷的概率为$\frac{2}{5}$.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握恩威是否同意限定区域停车与家长的性别有关?请说明理由.
附临界表及参考公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 同一限定区域停车 | 不同一限定区域停车 | 合计 | |
| 男 | 5 | ||
| 女 | 10 | ||
| 合计 | 50 |
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握恩威是否同意限定区域停车与家长的性别有关?请说明理由.
附临界表及参考公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
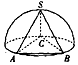 如图,已知底面为正三角形,侧棱长都相等的三棱锥S-ABC各顶点都在半球面上,其中A、B、C三顶点在底面圆周上,若三棱锥S-ABC的体积为2$\sqrt{3}$,则该半球的体积为$\frac{16π}{3}$.
如图,已知底面为正三角形,侧棱长都相等的三棱锥S-ABC各顶点都在半球面上,其中A、B、C三顶点在底面圆周上,若三棱锥S-ABC的体积为2$\sqrt{3}$,则该半球的体积为$\frac{16π}{3}$.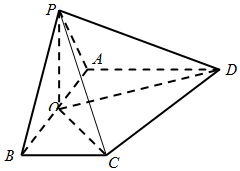 如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3
如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3