题目内容
6.已知E(1,0),K(-1,0),P是平面上一动点,且满足$|\overrightarrow{PE}|•|\overrightarrow{KE}|=\overrightarrow{PK}•\overrightarrow{EK}$.(1)求点P的轨迹C对应的方程;
(2)过点K的直线l与C相交于A、B两点(A点在x轴上方),点A关于x轴的对称点为D,且$\overrightarrow{EA}•\overrightarrow{EB}=-8$,求△ABD的外接圆的方程.
分析 (1)设P(x,y),则$\overrightarrow{PE}=(1-x,-y)$,$\overrightarrow{PK}=(-1-x,-y)$,$\overrightarrow{EK}=(-2,0)$,$\overrightarrow{KR}=(2,0)$.由P是平面上一动点,且满足$|\overrightarrow{PE}|•|\overrightarrow{KE}|=\overrightarrow{PK}•\overrightarrow{EK}$.能求出点P的轨迹C对应的方程.
(2)设l的方程为x=my-1(m>0).将x=my-1代入y2=4x并整理得y2-4my+4=0,由此利用根的判别式、韦达定理、中点坐标公式、点到直线距离公式、弦长公式,结合题意能求出△ABD的外接圆M的方程.
解答 解:(1)设P(x,y),$\overrightarrow{PE}=(1-x,-y)$,
$\overrightarrow{PK}=(-1-x,-y)$,$\overrightarrow{EK}=(-2,0)$,$\overrightarrow{KR}=(2,0)$.
∵$|\overrightarrow{PE}|•|\overrightarrow{KE}|=\overrightarrow{PK}•\overrightarrow{EK}$,
∴$2\sqrt{{{(1-x)}^2}+{y^2}}=2(x+1)$,
整理,得点P的轨迹C对应的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),D(x1,-y1),
l的方程为x=my-1(m>0).
将x=my-1代入y2=4x并整理得y2-4my+4=0,
由△>0,解得m>1,从而y1+y2=4m,y1y2=4.
x1+x2=(my1-1)+$(m{y_2}-1)=4{m^2}-2$,${x_1}{x_2}=\frac{{{y_1}^2{y_2}^2}}{16}=1$.
∵$\overrightarrow{EA}=({x_1}-1,{y_1})$,$\overrightarrow{EB}=({x_2}-1,{y_2})$,
∴$\overrightarrow{EA}•\overrightarrow{EB}=({x_1}-1)({x_2}-1)+{y_1}{y_2}$=${x_1}{x_2}-({x_1}+{x_2})+1+4=8-4{m^2}$.
∴8-4m2=-8,解得m=2,∴l的方程为x-2y+1=0.
设AB中点为(x0,y0),
则${x_0}=\frac{{{x_1}+{x_2}}}{2}=2{m^2}-1=7$,${y_0}=\frac{{{y_1}+{y_2}}}{2}=2m=4$,AB中垂线方程y-4=-2(x-7).
令y=0得x=9,圆心坐标(9,0),到AB的距离为$2\sqrt{5}$.
$|AB|=\sqrt{1+{m^2}}\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=4\sqrt{15}$.
圆的半径$r=\sqrt{{{(2\sqrt{15})}^2}-{{(2\sqrt{5})}^2}}=2\sqrt{10}$,
△ABD的外接圆M的方程(x-9)2+y2=40.
点评 本题考查点的轨迹方程式、圆的方程的求法,考查抛物线、圆的概念、性质的应用,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题,解题时要认真审题,注意根的判别式、韦达定理、中点坐标公式、点到直线距离公式、弦长公式的合理运用.

| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
| A. | 在[-π,π]上是增函数 | B. | 在[0,π]上是减函数 | ||
| C. | 在$[{-\frac{π}{2},\frac{π}{2}}]$上是减函数 | D. | 在[-π,0]上是减函数 |
| A. | $y=4sin(2x+\frac{π}{6})$ | B. | $y=-2sin(2x+\frac{π}{6})+2$ | C. | $y=-2sin(x+\frac{π}{3})+2$ | D. | $y=2sin(2x+\frac{π}{3})+2$ |
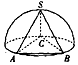 如图,已知底面为正三角形,侧棱长都相等的三棱锥S-ABC各顶点都在半球面上,其中A、B、C三顶点在底面圆周上,若三棱锥S-ABC的体积为2$\sqrt{3}$,则该半球的体积为$\frac{16π}{3}$.
如图,已知底面为正三角形,侧棱长都相等的三棱锥S-ABC各顶点都在半球面上,其中A、B、C三顶点在底面圆周上,若三棱锥S-ABC的体积为2$\sqrt{3}$,则该半球的体积为$\frac{16π}{3}$.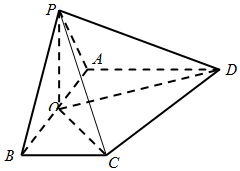 如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3
如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3