题目内容
16.“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 关于x的方程x2-mx+n=0有两个正根,则$\left\{\begin{array}{l}{△={m}^{2}-4n≥0}\\{m>0}\\{n>0}\end{array}\right.$.方程mx2+ny2=1的曲线是椭圆,则$\left\{\begin{array}{l}{m>0,n>0}\\{m≠n}\end{array}\right.$.即可得出结论.
解答 解:关于x的方程x2-mx+n=0有两个正根,则$\left\{\begin{array}{l}{△={m}^{2}-4n≥0}\\{m>0}\\{n>0}\end{array}\right.$.
方程mx2+ny2=1的曲线是椭圆,则$\left\{\begin{array}{l}{m>0,n>0}\\{m≠n}\end{array}\right.$.
上述两个不等式组相互推不出.
∴关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的既不充分也不必要条件.
故选:D.
点评 本题考查了方程与判别式的关系、椭圆的标准方程、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知向量$\overrightarrow{m}$,$\overrightarrow{n}$分别是直线l和平面α的方向向量和法向量,若$\overrightarrow{m}$与$\overrightarrow{n}$夹角的余弦等于$\frac{1}{2}$,则l与α所成的角为( )
| A. | 60° | B. | 30° | C. | 120° | D. | 150° |
11.已知命题p:?x∈R,3x-3≤0.若(¬p)∧q是假命题,则命题q可以是( )
| A. | 抛物线y=$\frac{1}{4}$x2的焦点坐标为(0,1) | |
| B. | 双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=2的右顶点到其左、右焦点的距离之比为3 | |
| C. | 函数f(x)=x3-3x2+b在区间(-∞,-1)上无极值点 | |
| D. | 曲线f(x)=x3-3x2+5在点(1,f(1))处切线的倾斜角大于$\frac{3π}{4}$ |
1.某篮球运动员在最近5场比赛中所得分数分别为12,a,8,15,23,其中a>0,若该运动员在这5场比赛中得分的中位数为12,则得分的平均数不可能为( )
| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | $\frac{71}{5}$ | D. | 14 |
8.某几何体的三视图如图所示,则该几何体的体积是( )
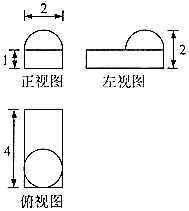

| A. | 8+$\frac{4}{3}$π | B. | 8+$\frac{2}{3}$π | C. | 4+$\frac{4π}{3}$ | D. | 4+$\frac{2π}{3}$ |
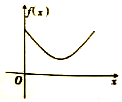
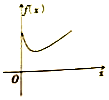
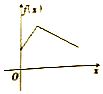
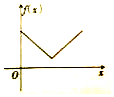
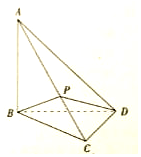 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )