题目内容
6．设A（x1，y1），B（x2，y2），C（x3，y3）是函数y=x3的图象上任意三个不同的点．求证：若A，B，C三点共线，则x1+x2+x3=0．分析 kAB=$\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}-{x}_{1}}$，kAC=$\frac{{x}_{3}^{3}-{x}_{1}^{3}}{{x}_{3}-{x}_{1}}$．由A，B，C三点共线，可得kAB=kAC．化简整理即可得出．
解答 证明：kAB=$\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}-{x}_{1}}$，kAC=$\frac{{x}_{3}^{3}-{x}_{1}^{3}}{{x}_{3}-{x}_{1}}$．
∵A，B，C三点共线，∴kAB=kAC．
∴$\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}-{x}_{1}}$=$\frac{{x}_{3}^{3}-{x}_{1}^{3}}{{x}_{3}-{x}_{1}}$．
∴${x}_{2}^{2}$+x1x2+${x}_{1}^{2}$=${x}_{3}^{2}$+x1x3+${x}_{1}^{2}$，
∴（x2-x3）（x1+x2+x3）=0，∵x2≠x3．
∴x1+x2+x3=0．
点评 本题考查了直线共线与斜率的关系、乘法公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
16．“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
17．将二项式${（x+\frac{2}{{\sqrt{x}}}）^6}$展开式各项重新排列，则其中无理项互不相邻的概率是（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{1}{35}$ | C． | $\frac{8}{35}$ | D． | $\frac{7}{24}$ |
14．为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班进行教学实验，为了解教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图，记成绩不低于70分者为“成绩优良”．
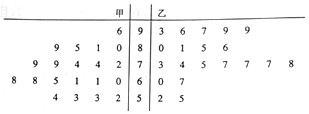
（1）分别计算甲、乙两班20个样本中，化学分数前十的平均分，并据此判断哪种教学方式的教学效果更
佳；
（2）甲、乙两班40个样本中，成绩在60分以下的学生中任意选取2人，求这2人来自不同班级的概率；
（3）由以上统计数据填写下面2×2列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+c）（b+d）（a+b）（c+d）}，（n=a+b+c+d）$
独立性检验临界值表：
（1）分别计算甲、乙两班20个样本中，化学分数前十的平均分，并据此判断哪种教学方式的教学效果更
佳；
（2）甲、乙两班40个样本中，成绩在60分以下的学生中任意选取2人，求这2人来自不同班级的概率；
（3）由以上统计数据填写下面2×2列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”？
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
独立性检验临界值表：
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
1．若复数z满足$（{\sqrt{2}+i}）z=3i$（i为虚数单位），则z的共轭复数为（ ）
| A． | $\sqrt{2}+i$ | B． | $\sqrt{2}-i$ | C． | $1+\sqrt{2}i$ | D． | $1-\sqrt{2}i$ |
9．已知直线l1：y=ax-2a+5过定点A，则点A到直线l：x-2y+3=0的距离为（ ）
| A． | $2\sqrt{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\sqrt{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$ |