题目内容
8.某几何体的三视图如图所示,则该几何体的体积是( )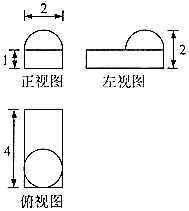
| A. | 8+$\frac{4}{3}$π | B. | 8+$\frac{2}{3}$π | C. | 4+$\frac{4π}{3}$ | D. | 4+$\frac{2π}{3}$ |
分析 由已知中的三视图可得:该几何体是一个四棱柱与半球的组合体,进而得到答案.
解答 解:由已知中的三视图可得:该几何体是一个四棱柱与半球的组合体,
故体积V=1×2×4+$\frac{1}{2}$×$\frac{4}{3}π$=8+$\frac{2}{3}$π,
故选:B.
点评 本题考查的知识点是球的体积与表面积,棱柱的体积与表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
16.“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.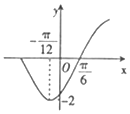 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
20.已知函数f(x)=x$({{e^x}-\frac{1}{e^x}})$,若f(x1)<f(x2),则( )
| A. | x1>x2 | B. | x1<x2 | C. | ${x}_{1}^{2}$<${x}_{2}^{2}$ | D. | x1+x2=0 |
17.将二项式${(x+\frac{2}{{\sqrt{x}}})^6}$展开式各项重新排列,则其中无理项互不相邻的概率是( )
| A. | $\frac{2}{7}$ | B. | $\frac{1}{35}$ | C. | $\frac{8}{35}$ | D. | $\frac{7}{24}$ |
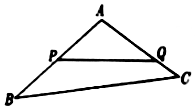 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.