题目内容
已知向量
=(sin2x,-
),
=(
,cos2x)设f(x)=2
•
.
(1)求f(x)的最大值,并求最大值所对应的自变量;
(2)令g(x)=
x2-x,对任意x1∈[-
,
],存在x2∈[-
,
]时,使λ•g(x1)=f(x2)成立,求实数λ的取值范围.
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
| a |
| b |
(1)求f(x)的最大值,并求最大值所对应的自变量;
(2)令g(x)=
| 2 |
| π |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:分类讨论,三角函数的图像与性质,平面向量及应用
分析:(1)利用平面向量的数量积以及三角函数的恒等变换,求出f(x)的最大值以及对应的自变量x的取值;
(2)求出g(x)在x1∈[-
,
]上的值域,f(x2)在x2∈[-
,
]上的值域;
讨论λ的取值,求出使λ•g(x1)=f(x2)时λ的取值范围.
(2)求出g(x)在x1∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
讨论λ的取值,求出使λ•g(x1)=f(x2)时λ的取值范围.
解答:
解:(1)∵
=(sin2x,-
),
=(
,cos2x),
∴f(x)=2
•
=2(
sin2x-
cos2x)
=2sin(2x-
);
当2x-
=2kπ+
,
即x=kπ+
(k∈Z)时,f(x)取得最大值2;
(2)∵g(x)=
x2-x
=
(x-
)2-
,
∴当x=
时,g(x)取得最小值g(x)min=-
,
当x=-
时,g(x)取得最大值g(x)max=π;
∴g(x)的值域是[-
,π];
又∵-
≤2x-
≤
,
∴f(x2)的值域是[-2,2];
当λ≥0时,λ•g(x1)∈[-
λ,πλ],
由已知[-
λ,πλ]⊆[-2,2],
∴
,
解得0≤λ≤
;
当λ<0时,λ•g(x1)∈[πλ,-
λ],
同理可得-
≤λ<0;
综上,λ的取值范围是[-
,
].
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
∴f(x)=2
| a |
| b |
=2(
| 1 |
| 2 |
| ||
| 2 |
=2sin(2x-
| π |
| 3 |
当2x-
| π |
| 3 |
| π |
| 2 |
即x=kπ+
| 5π |
| 12 |
(2)∵g(x)=
| 2 |
| π |
=
| 2 |
| π |
| π |
| 4 |
| π |
| 8 |
∴当x=
| π |
| 4 |
| π |
| 8 |
当x=-
| π |
| 2 |
∴g(x)的值域是[-
| π |
| 8 |
又∵-
| 4π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴f(x2)的值域是[-2,2];
当λ≥0时,λ•g(x1)∈[-
| π |
| 8 |
由已知[-
| π |
| 8 |
∴
|
解得0≤λ≤
| 2 |
| π |
当λ<0时,λ•g(x1)∈[πλ,-
| π |
| 8 |
同理可得-
| 2 |
| π |
综上,λ的取值范围是[-
| 2 |
| π |
| 2 |
| π |
点评:本题考查了平面向量的应用问题,也考查了三角函数的恒等变换以及函数的图象与性质的应用问题,是综合题.

练习册系列答案
相关题目
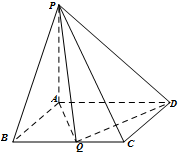 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)