题目内容
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
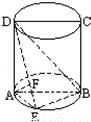
(1)求证:AF⊥DB;
(2)如果圆柱与三棱锥D﹣ABE的体积的比等于3π,求直线DE与平面ABCD所成的角.
(1)见解析;(2)arcctg( /5)
/5)
【解析】
试题分析:(1)欲证AF⊥DB,先证AF⊥平面DEB,根据线面垂直的判定定理可知只需证EB⊥AF,AF⊥DE,且EB∩DE=E,即可证得线面垂直;
(2)点E作EH⊥AB,H是垂足,连接DH,易证∠EDH是DE与平面ABCD所成的角,在三角形EDH中求出此角即可.
(1)证明:根据圆柱性质,DA⊥平面ABE.
∵EB?平面ABE,
∴DA⊥EB.
∵AB是圆柱底面的直径,点E在圆周上,
∴AE⊥EB,又AE∩AD=A,
故得EB⊥平面DAE.
∵AF?平面DAE,
∴EB⊥AF.
又AF⊥DE,且EB∩DE=E,
故得AF⊥平面DEB.
∵DB?平面DEB,
∴AF⊥DB.
(2)【解析】
过点E作EH⊥AB,H是垂足,连接DH.
根据圆柱性质,平面ABCD⊥平面ABE,AB是交线.且EH?平面ABE,所以EH⊥平面ABCD.
又DH?平面ABCD,所以DH是ED在平面ABCD上的射影,从而∠EDH是DE与平面ABCD所成的角.
设圆柱的底面半径为R,则DA=AB=2R,于是
V圆柱=2πR3, .
.
由V圆柱:VD﹣ABE=3π,得EH=R,可知H是圆柱底面的圆心,
AH=R,
DH=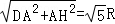
∴∠EDH=arcctg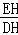 =arcctg(
=arcctg( /5),
/5),



练习册系列答案
相关题目
 设
设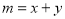 ,若
,若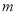 的最大值为6,则
的最大值为6,则 的最小值为( )
的最小值为( ) ,
,
 ,若
,若 ,则
,则 的最小值为
的最小值为 B.
B. C.
C. D.
D.
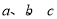 成等比数列的充要条件是
成等比数列的充要条件是
 的等比数列是递减数列
的等比数列是递减数列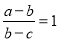 是
是 成等差数列的充分不必要条件
成等差数列的充分不必要条件 是满足
是满足 的整数,若
的整数,若 成等比数列,则
成等比数列,则 的值依次为__________.
的值依次为__________.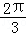 ,则线段AB的长度为( )
,则线段AB的长度为( ) C.2 D.2
C.2 D.2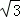
 ,要得到
,要得到 f′(x)的图象,只需将f(x)的图象( )个单位.
f′(x)的图象,只需将f(x)的图象( )个单位. B.向左平移
B.向左平移 D.向左平移
D.向左平移