题目内容
14.在菱形ABCD中,AB=2,∠DAB=60°,E为CD的中点,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的值是5.分析 运用向量的中点表示和加减运算,以及向量数量积的定义及性质:向量的平方即为模的平方,计算即可得到所求值.
解答 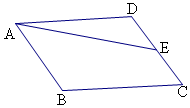 解:∵E为CD的中点,
解:∵E为CD的中点,
∴$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{AB}$,
∴$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,
又ABCD为菱形,且AB=2,
∠DAB=60°,
∴$\overrightarrow{AD}•\overrightarrow{AE}=\overrightarrow{AD}•({\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}})={|{\overrightarrow{AD}}|^2}+\frac{1}{2}\overrightarrow{AD}•\overrightarrow{AB}=4+\frac{1}{2}×2×2×\frac{1}{2}=5$.
故答案为:5.
点评 本题考查向量数量积的定义和性质,同时考查向量的加减运算,中点向量的表示形式,考查运算能力,属于基础题.

练习册系列答案
相关题目
5.已知点A(2,-1,2),B(4,5,-1),C(-2,2,3),且$\overrightarrow{AP}=\frac{1}{2}\overrightarrow{CB}$,则P点的坐标为( )
| A. | (5,5,0) | B. | $(5,\frac{1}{2},0)$ | C. | $(-1,\frac{1}{2},0)$ | D. | (-1,5,0) |
4.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( )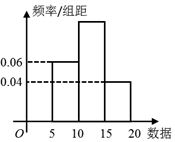

| A. | 12.5 11 | B. | 12.5 12 | C. | 12.5 13 | D. | 12.5 14 |