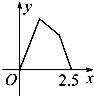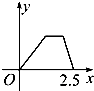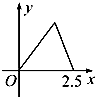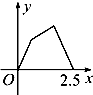题目内容
已知函数f(x)=ax+
(a>1).
(1)判定函数f(x)在(-1,+∞)上的单调性,并给出证明;
(2)证明:方程f(x)=0没有负数根.
| x-2 |
| x+1 |
(1)判定函数f(x)在(-1,+∞)上的单调性,并给出证明;
(2)证明:方程f(x)=0没有负数根.
考点:函数的零点,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)设x1,x2∈(-1,+∞),且x1<x2,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义,得到答案.
(2)假设f(x)=0 有负根 x0,即 f(x0)=0,根据f(0)=-1,可得 f(x0)>f(0)①,若-1<x0<0,由条件可得f(x0)<f(0)=-1,这与①矛盾,若x0<-1,可得 f(x0)>0,这也与①矛盾.
(2)假设f(x)=0 有负根 x0,即 f(x0)=0,根据f(0)=-1,可得 f(x0)>f(0)①,若-1<x0<0,由条件可得f(x0)<f(0)=-1,这与①矛盾,若x0<-1,可得 f(x0)>0,这也与①矛盾.
解答:
解:(1)函数在f(x)在(-1,+∞)上为增函数.
证明如下:设x1,x2∈(-1,+∞),且x1<x2,
∵a>1,
∴ax1-ax2<0,x1-x2<0,x1+1>0,x2+1>0
∴f(x1)-f(x2)=(ax1+
)-(ax2+
)=(ax1-ax2)+[
-
]=(ax1-ax2)+
<0,
f(x1)<f(x2)
∴函数f(x)在(-1,+∞)上为增函数.
证明:(2)假设f(x)=0 有负根 x0,且 x0≠-1,即 f(x0)=0.
根据f(0)=1+
=-1,可得 f(x0)>f(0)①.
若-1<x0<0,由函数f(x)=ax+
在(-1,+∞)是增函数,可得f(x0)<f(0)=-1,这与①矛盾.
若x0<-1,则 ax0>0,x0-2<0,x0+1<0,∴f(x0)>0,这也与①矛盾.
故假设不正确.
∴方程 ax+
=0 没有负根.
证明如下:设x1,x2∈(-1,+∞),且x1<x2,
∵a>1,
∴ax1-ax2<0,x1-x2<0,x1+1>0,x2+1>0
∴f(x1)-f(x2)=(ax1+
| x1-2 |
| x1+1 |
| x2-2 |
| x2+1 |
| (x1-2)(x2+1) |
| (x1+1)(x2+1) |
| (x2-2)(x1+1) |
| (x1+1)(x2+1) |
| 3(x1-x2) |
| (x1+1)(x2+1) |
f(x1)<f(x2)
∴函数f(x)在(-1,+∞)上为增函数.
证明:(2)假设f(x)=0 有负根 x0,且 x0≠-1,即 f(x0)=0.
根据f(0)=1+
| 0-2 |
| 0+1 |
若-1<x0<0,由函数f(x)=ax+
| x-2 |
| x+1 |
若x0<-1,则 ax0>0,x0-2<0,x0+1<0,∴f(x0)>0,这也与①矛盾.
故假设不正确.
∴方程 ax+
| x-2 |
| x+1 |
点评:本题考查的知识点是函数单调性的证明,用反证法证明数学命题,推出矛盾,是解题的关键和难点.

练习册系列答案
相关题目
已知函数f(x+1)的定义域为[1,2],则函数y=f(
)的定义域为( )
| x+1 |
| A、[1,2] |
| B、[2,4] |
| C、[3,8] |
| D、[5,10] |
已知f(x)为R上的减函数,则满足f(2x-1)<f(1)的实数x的取值范围是 ( )
| A、(-∞,-1) |
| B、(-1,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
复数z=1+i,则
+z=( )
| 1 |
| z |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
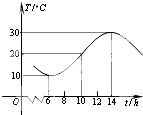 如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.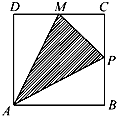 如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )
如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )