题目内容
已知命题p：?x∈R，有3x＜2x成立；命题q：?x∈（0，+∞），恒有sinx+
≥2成立，则下列命题为真命题的是（ ）
| 1 |
| sinx |
| A、p∧q |
| B、（￢p）∨q |
| C、p∧（￢q） |
| D、（￢p）∧（￢q） |
考点：复合命题的真假
专题：计算题
分析：先判断命题p、q的真假，再根据复合命题真值表依次判断可得答案．
解答：
解：∵当0＜x＜1时，3x＜2x，∴命题p为真命题；
∵sinx＜0时，sinx+
＜0，∴命题q为假命题，
由复合命题真值表得：p∧q为假命题；（￢p）∨q是假命题；p∧（￢q）为真命题；（￢p）∧（￢q）为假命题．
故选C．
∵sinx＜0时，sinx+
| 1 |
| sinx |
由复合命题真值表得：p∧q为假命题；（￢p）∨q是假命题；p∧（￢q）为真命题；（￢p）∧（￢q）为假命题．
故选C．
点评：本题考查了复合命题的真假判定，熟练记忆复合命题真值表是关键．
练习册系列答案
相关题目
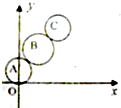我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”．在如图所示的“串圆”中，⊙A和⊙C的方程分别为x2+（y-1）2=2和（x-6）2+（y-7）2=2，则⊙B的方程为