题目内容
14.若a=2,则(1+ax)5的展开式中x3项的系数为80.分析 利用通项公式即可得出.
解答 解:通项公式Tr+1=${∁}_{5}^{r}(ax)^{r}$=ar${∁}_{5}^{r}$xr,则r=3.
令${a}^{3}{∁}_{5}^{3}$=80,解得a=2.
故答案为:2.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2.函数$y=\frac{lnx}{x}$的导数为( )
| A. | $y=\frac{1-lnx}{x^2}$ | B. | $y=\frac{1+lnx}{x^2}$ | C. | $y=\frac{lnx-1}{x^2}$ | D. | $y=\frac{x+lnx}{x^2}$ |
9.在空间中,下列命题中不正确的是( )
| A. | 若两个平面有一个公共点,则它们有无数个公共点 | |
| B. | 任意两条直线能确定一个平面 | |
| C. | 若点A既在平面α内,又在平面β内,则α与β相交于直线b,且点A在直线b上 | |
| D. | 若已知四个点不共面,则其中任意三点不共线 |
6.已知抛物线C的顶点在原点,焦点为F(-3,0),C上一点P到焦点F的距离为9,则点P的一个坐标为( )
| A. | (-3,6) | B. | (-3,6$\sqrt{2}$) | C. | (-6,6) | D. | (-6,6$\sqrt{2}$) |
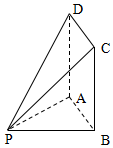 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.