题目内容
19.设方程f(x)=x-ln(ax)=0(a≠0,e为自然对数的底数),则( )| A. | 当a<0时,方程没有实数根 | B. | 当0<a<e时,方程有一个实数根 | ||
| C. | 当a=e,方程有三个实数根 | D. | 当a>e时,方程有两个实数根 |
分析 讨论a的符号,得出f(x)的定义域,利用导数判断f(x)的单调性,计算f(x)的极值,从而判断f(x)=0的解得个数情况.
解答 解:f′(x)=1-$\frac{1}{x}$,
由函数有意义得ax>0,
(1)若a<0,则x<0,
∴f′(x)>0,∴f(x)在(-∞,0)上单调递增,
当x→0时,f(x)→+∞,当x→-∞时,f(x)→-∞,
∴当a<0时,f(x)=0一点有一解;
(2)若a>0,则x>0,令f′(x)=0的x=1.
∴当0<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x=1时,f(x)取得最小值f(1)=1-lna,
又x→0时,f(x)→+∞,当x→+∞时,f(x)→+∞,
∴当1-lna=0即a=e时,f(x)=0只有一解x=1;
当1-lna>0即0<a<e时,f(x)=0无解;
当1-lna<0即a>e时,f(x)=0有两解.
古选D.
点评 本题考查了方程根的个数与函数单调性、极值的关系,分类讨论思想,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
10.利用独立性检验来考察两个分类变量X和Y是否有关系时,通过查阅表来确定“X与Y有关系”的可信程度.
如果K2>5.024,那么就有把握认为“X与Y有关系”的百分比为( )
| P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 25% | B. | 75% | C. | 2.5% | D. | 97.5% |
4.三棱锥P-ABC的四个顶点均在半径为5的球面上,且△ABC是斜边长为8的等腰直角三角形,则三棱锥P-ABC的体积的最大值为( )
| A. | 64 | B. | 128 | C. | $\frac{64}{3}$ | D. | $\frac{128}{3}$ |
11.若数列{an},{bn}的通项公式分别为an=(-1)n+2016•a,bn=2+$\frac{{{{(-1)}^{n+2017}}}}{n}$,且an<bn,对任意n∈N*恒成立,则实数a的取值范围是( )
| A. | $[-1,\frac{1}{2})$ | B. | [-1,1) | C. | [-2,1) | D. | $[-2,\frac{3}{2})$ |
8.执行如图所示的程序框图,如果输入n=3,则输出的S值为( )
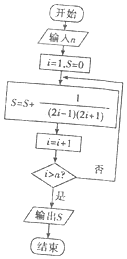

| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |