题目内容
9.tanα+$\frac{1}{tanα}$=$\frac{9}{4}$,则求tan2α+$\frac{1}{sinαcosα}$+$\frac{1}{ta{n}^{2}α}$的值.分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵tanα+$\frac{1}{tanα}$=$\frac{9}{4}$,∴tan2α+$\frac{1}{sinαcosα}$+$\frac{1}{{tan}^{2}α}$=${(tanα+\frac{1}{tanα})}^{2}$-2+$\frac{{sin}^{2}α{+cos}^{2}α}{sinαcosα}$=${(\frac{9}{4})}^{2}$-2+tanα+$\frac{1}{tanα}$=$\frac{85}{16}$.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
19.某算法的程序框图如图所示,若输x的值为2,则输出y的值是( )
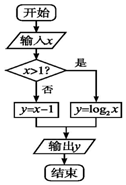

| A. | 1 | B. | 2 | C. | 4 | D. | 以上都不对 |
17.平面内给定三个向量$\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(-1,2),$\overrightarrow{c}$=(4,1),若($\overrightarrow{a}$+k$\overrightarrow{c}$)∥(2$\overrightarrow{b}$-$\overrightarrow{a}$)则实数k的值为( )
| A. | $\frac{16}{13}$ | B. | $\frac{3}{4}$ | C. | $-\frac{16}{13}$ | D. | $-\frac{4}{3}$ |
19.设方程f(x)=x-ln(ax)=0(a≠0,e为自然对数的底数),则( )
| A. | 当a<0时,方程没有实数根 | B. | 当0<a<e时,方程有一个实数根 | ||
| C. | 当a=e,方程有三个实数根 | D. | 当a>e时,方程有两个实数根 |