题目内容
14.函数$y={log_{\frac{1}{2}}}({x^2}-4x-5)$的递增区间为(-∞,-1).分析 由已知中函数y=log0.5(x2-4x-5)的解析式,先确定函数的定义域,进而根据二次函数和对数函数的性质,分别判断内,外函数的单调性,进而根据复合函数“同增异减”的原则,得到答案.
解答 解:函数y=log0.5(x2-4x-5)的定义域为(-∞,-1)∪(5,+∞)
令t=x2-4x-5,则y=log0.5t,
∵y=log0.5t为减函数,
t=x2-4x-5的单调递减区间是(-∞,2),单调递增区间是(2,+∞)
故函数y=log0.5(x2-4x-5)的单调递增区间是(-∞,-1).
故答案为:(-∞,-1).
点评 本题考查的知识点是二次函数的图象和性质,对数函数的单调区间,复合函数的单调性,其中复合函数单调性“同增异减”的原则,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.设方程f(x)=x-ln(ax)=0(a≠0,e为自然对数的底数),则( )
| A. | 当a<0时,方程没有实数根 | B. | 当0<a<e时,方程有一个实数根 | ||
| C. | 当a=e,方程有三个实数根 | D. | 当a>e时,方程有两个实数根 |
5.$(x+\frac{1}{x}){(ax-1)^5}$的展开式中各项系数的和为2,则该展开式中常数项为( )
| A. | -20 | B. | -10 | C. | 10 | D. | 20 |
2.设α、β、γ为平面,m、n、l为直线,则能推m⊥β是( )
| A. | α⊥β,α∩β=l,m⊥l | B. | α∩γ=m,α⊥γ,β⊥γ | C. | α⊥γ,β⊥γ,m⊥α | D. | n⊥α,n⊥β,m⊥α |
3.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
已知在全部50人中随机抽取1人,抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
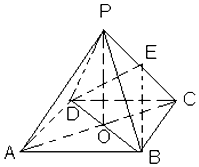 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: