题目内容
已知二次函数f(x)=ax2+bx+c(a>0)的图象与x轴有两个不同的交点.若f(c)=0,且0<x<c时,f(x)>0.
(1)证明: 是函数f(x)的一个零点;
是函数f(x)的一个零点;
(2)试比较 与c的大小.
与c的大小.
解:(1)证明:∵f(x)的图象与x轴有两个不同的交点,
∴f(x)=0有两个不等实根x1,x2,
∵f(c)=0,∴x1 =c是f(x)=0的根,
=c是f(x)=0的根,
又x1x2= ,∴x2=
,∴x2= (
( ≠c),
≠c),
∴ 是f(x)=0的一个根.即
是f(x)=0的一个根.即 是函数f(x)的一个零点.
是函数f(x)的一个零点.
(2)假设 <c,∵
<c,∵ >0,由0<x<c时,f(x)>0,知f(
>0,由0<x<c时,f(x)>0,知f( )>0,
)>0,
这与f( )=0矛盾,∴
)=0矛盾,∴ ≥c,又∵
≥c,又∵ ≠c,∴
≠c,∴ >c.
>c.

练习册系列答案
相关题目
 0,则
0,则 的最小值是( )
的最小值是( )
 >b+
>b+ B.
B. >
> 
 >
>

 +4×33+…+n×3n-1=3n(na-b)+c对一切n∈N*都成立,则a、b、c的值为( )
+4×33+…+n×3n-1=3n(na-b)+c对一切n∈N*都成立,则a、b、c的值为( )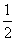 ,b=c=
,b=c= B.a=b=c=
B.a=b=c=