题目内容
函数f(x)=2x-
为偶函数,则下列函数中在区间(0,2)上递减的是( )
| a |
| 2x |
| A、f(x)=x2+2ax-1 | ||
| B、f(x)=(1-a)x | ||
| C、f(x)=-ax3-12x+1 | ||
D、f(x)=x-
|
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数是偶函数,求出a的值,即可得到结论.
解答:
解:∵f(x)=2x-
为偶函数,
∴f(-x)=f(x),
即2-x-
=2x-
,
即2x-
=
-a•2x,
即a=-1,
则A.f(x)=x2+2ax-1=f(x)=x2-2x-1,对称轴为x=1,则区间(0,2)上不单调,不满足条件.
B.f(x)=(1-a)x=2x,在区间(0,2)上递增,不满足条件,
C.f(x)=-ax3-12x+1=x3-12x+1,函数的f′(x)=3x2-12=3(x2-4),
则当0<x<2时,f′(x)<0,函数单调递减,满足条件.
D.f(x)=x-
=x+
,在区间(0,2)上不单调,不满足条件,
故选:C
| a |
| 2x |
∴f(-x)=f(x),
即2-x-
| a |
| 2-x |
| a |
| 2x |
即2x-
| a |
| 2x |
| 1 |
| 2x |
即a=-1,
则A.f(x)=x2+2ax-1=f(x)=x2-2x-1,对称轴为x=1,则区间(0,2)上不单调,不满足条件.
B.f(x)=(1-a)x=2x,在区间(0,2)上递增,不满足条件,
C.f(x)=-ax3-12x+1=x3-12x+1,函数的f′(x)=3x2-12=3(x2-4),
则当0<x<2时,f′(x)<0,函数单调递减,满足条件.
D.f(x)=x-
| a |
| x |
| 1 |
| x |
故选:C
点评:本题主要考查函数奇偶性和单调性的应用,综合考查函数的性质.

练习册系列答案
相关题目
△ABC,若asinA=bsinB,则△ABC的形状为( )
| A、等腰三角形 |
| B、等腰直角三角形 |
| C、直角三角形 |
| D、等边三角形 |
函数f(x)=log2(x+
)(x∈R)的奇偶性为( )
| x2+1 |
| A、偶函数 |
| B、奇函数 |
| C、非奇非偶函数 |
| D、既是奇函数又是偶函数 |
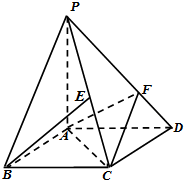 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,E为PC中点,PF=2FD,求证:BE∥平面AFC.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,E为PC中点,PF=2FD,求证:BE∥平面AFC.