题目内容
16.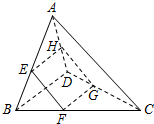 如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )
如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )| A. | 函数f(x)的值域为(0,1] | B. | 函数y=f(x)满足f(x)=f(2-x) | ||
| C. | 函数y=f(x)的最大值为2 | D. | 函数y=f(x)在(0,$\frac{1}{2}$)上单调递增 |
分析 根据空间四边形的性质证明四边形EFGH为矩形,然后根据比例关系求出函数f(x)的表达式,结合一元二次函数的性质进行判断即可.
解答 解:∵AC∥平面EFGH,BD∥平面EFGH,
∴AC∥EF.AC∥HG,BD∥EH.BD∥FG,
则四边形EFGH为平行四边形,
∵AC,BD互相垂直,
∴EH⊥EF,
则四边形EFGH为矩形,
∵$\frac{BE}{AB}$=x,
∴由$\frac{EH}{BD}$=$\frac{AE}{AB}$=$\frac{AB-BE}{AB}$=1-$\frac{BE}{AB}$=1-x,
即EH=(1-x)BD=3(1-x),
同理 $\frac{EF}{AC}$=$\frac{BE}{AB}$=x,
则EF=x•AC=2x,
则四边形EFGH的面积为y=EH•EF=2x•3(1-x)=6(x-x2)=-6(x-$\frac{1}{2}$)2+$\frac{3}{2}$,
∵x∈(0,1),
∴当x=$\frac{1}{2}$时,函数取得最大值$\frac{3}{2}$,故A,C错误.
函数y=f(x)=6(x-x2)=-6(x-$\frac{1}{2}$)2+$\frac{3}{2}$在(0,$\frac{1}{2}$)上单调递增,故D正确.
∵函数的对称轴为x=$\frac{1}{2}$,
∴函数y=f(x)满足f(x)=f(1-x),故B错误.
故选:D.
点评 本题主要考查空间四边形和函数的综合以及与一元二次函数有关的性质,综合性较强,涉及的知识点较多,有一点的难度,属于中档题.

练习册系列答案
相关题目
7.下列函数中,是奇函数的是( )
| A. | y=x2sin(x+$\frac{π}{3}$) | B. | y=x2cos$\frac{x}{3}$ | C. | y=tan(x-$\frac{π}{3}$) | D. | y=x3tanx2 |
4.设x0为函数f(x)=sinπx的零点,且满足|x0|+f(x0+$\frac{1}{2}$)<33,则这样的零点有( )
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |



