题目内容
14.在空间直角坐标系中,已知三点A(1,0,0),B(1,1,1),C(0,1,1),则三角形ABC 是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
分析 由空间两点间距离公式分别求出三边长,再由勾股定理能判断三角形的形状.
解答 解:∵三点A(1,0,0),B(1,1,1),C(0,1,1),
∴|AB|=$\sqrt{(1-1)^{2}+(0-1)^{2}+(0-1)^{2}}$=$\sqrt{2}$,
|AC|=$\sqrt{(0-1)^{2}+(1-0)^{2}+(1-0)^{2}}$=$\sqrt{3}$,
|BC|=$\sqrt{(0-1)^{2}+(1-1)^{2}+(1-1)^{2}}$=1,
∴AC2=AB2+BC2,
∴三角形ABC是直角三角形.
故选:A.
点评 本题考查三角形形状的判断,是基础题,解题时要认真审题,注意空间中两点间距离公式的合理运用.

练习册系列答案
相关题目
4.设x0为函数f(x)=sinπx的零点,且满足|x0|+f(x0+$\frac{1}{2}$)<33,则这样的零点有( )
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
2.设命题p:若2x>3x,则x<0,其逆否命题为( )
| A. | 若x≥0,则2x≤3x | B. | 若x>0,则 2x<3x | C. | 若2x>3x,则x≥0 | D. | 若2x≤3x,则x>0 |
9.已知正方体ABCD-A1B1C1D1中,E,F分别是A1D1,D1C1的中点,则异面直线EF与AB1所成角为( )
| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
4.某种型号的书包原价为a元,如果连续两次以相同的百分率x降价,那么两次降价后价格为多少元?( )
| A. | a(1-x) | B. | a(1-x)2 | C. | a(1-2x) | D. | 以上都不是 |




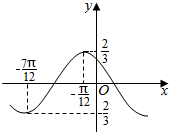 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示