题目内容
3.设存在三个点A(-2,2)、B(-1,4)、C(4,-5),且$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{CD}$,求点D的坐标.分析 设出D的坐标,表示出$\overrightarrow{AB},\overrightarrow{CD}$的坐标,根据$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{CD}$列出方程解出D的坐标.
解答 解:设D(x,y),则$\overrightarrow{AB}$=(1,2),$\overrightarrow{CD}$=(x-4,y+5),
∵$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{CD}$,∴$\left\{\begin{array}{l}{x-4=2}\\{y+5=4}\end{array}\right.$,解得x=6,y=-1.
∴D(6,-1).
点评 本题考查了平面向量的坐标运算,是基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.设a=40.8,b=80.46,c=($\frac{1}{2}$)-1.2,则a,b,c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
8.已知函数f(x)=mx-m2-1,m>0,x∈R.若a2+b2=1,则$\frac{f(b)}{f(a)}$的取值范围是( )
| A. | [$\frac{\sqrt{7}-4}{3}$,$\frac{\sqrt{7}+4}{3}$] | B. | (0,$\frac{4-\sqrt{7}}{3}$] | C. | [0,$\frac{4+\sqrt{7}}{3}$] | D. | [$\frac{4-\sqrt{7}}{3}$,$\frac{4+\sqrt{7}}{3}$] |
4.设x0为函数f(x)=sinπx的零点,且满足|x0|+f(x0+$\frac{1}{2}$)<33,则这样的零点有( )
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
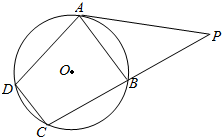 如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.
如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.