题目内容
9.已知ax-y+2a+1=0,当a∈[-1,$\frac{1}{3}$]时,恒有y>0,求x的取值范围.分析 将不等式恒成立转化为以a为主变量的不等式,构造函数,利用函数的性质即可得到结论
解答 解:∵ax-y+2a+1=0,
∴y=ax+2a+1;
当a∈[-1,$\frac{1}{3}$]时,恒有y>0,
即ax+2a+1>0在a∈[-1,$\frac{1}{3}$]时恒成立;
设f(a)=ax+2a+1,a∈[-1,$\frac{1}{3}$];
则$\left\{\begin{array}{l}{f(-1)>0}\\{f(\frac{1}{3})>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-x-2+1>0}\\{\frac{1}{3}x+\frac{2}{3}+1>0}\end{array}\right.$,
解得-5<x<-1;
∴x的取值范围是-5<x<-1.
点评 本题主要考查不等式恒成立问题,将不等式转化为以a为主变量,构造函数是解决本题的关键

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
8.已知函数f(x)=mx-m2-1,m>0,x∈R.若a2+b2=1,则$\frac{f(b)}{f(a)}$的取值范围是( )
| A. | [$\frac{\sqrt{7}-4}{3}$,$\frac{\sqrt{7}+4}{3}$] | B. | (0,$\frac{4-\sqrt{7}}{3}$] | C. | [0,$\frac{4+\sqrt{7}}{3}$] | D. | [$\frac{4-\sqrt{7}}{3}$,$\frac{4+\sqrt{7}}{3}$] |
4.设x0为函数f(x)=sinπx的零点,且满足|x0|+f(x0+$\frac{1}{2}$)<33,则这样的零点有( )
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
14.已知直线l1:$\frac{x}{m-2}$-$\frac{4m}{m-2}$y+2=0,l2:m2x+$\frac{y}{m}$-9=0.若l1⊥l2,则m的值是( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).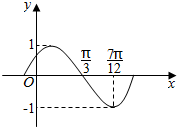 函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.