Question

10．已知函数f（x）=|x-l|+|x-3|．
（I）解不等式f（x）≤6；
（Ⅱ）若不等式f（x）≥ax-1对任意x∈R恒成立，求实数a的取值范围．

Answer 1

分析 （I）把不等式f（x）≤6等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．
（Ⅱ）由题意可得函数f（x）的图象不能在y=ax-1的图象的下方，数形结合求得a的范围．

解答 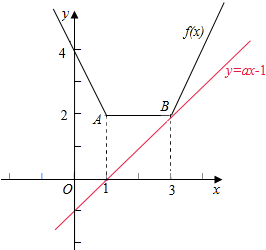解：函数f（x）=|x-l|+|x-3|=$\left\{\begin{array}{l}{-2x+4，x＜-1}\\{2，-1≤x≤3}\\{2x-4，x＞3}\end{array}\right.$ 的图象如图所示，

（I）不等式f（x）≤6，即$\left\{\begin{array}{l}{-2x+4≤6}\\{x＜-1}\end{array}\right.$①或$\left\{\begin{array}{l}{2x-4≤6}\\{x＞3}\end{array}\right.$②，或$\left\{\begin{array}{l}{2≤6}\\{-1≤x≤3}\end{array}\right.$③．
解①求得x∈∅，解②求得3＜x≤5，解③求得-1≤x≤3．
综上可得，原不等式的解集为[-1，5]．
（Ⅱ）若不等式f（x）≥ax-1对任意x∈R恒成立，则函数f（x）的图象
不能在y=ax-1的图象的下方．
如图所示：
由于图中两题射线的斜率分别为-2，2，点B（3，2），
∴3a-1≤2，且 a≥-2，求得-2≤a≤1．

点评 本题主要考查分段函数的应用，绝对值不等式的解法，体现了转化、数形结合的数学思想，属于中档题．