题目内容
19.定义在R上的函数f(x)满足f(x+2)=$\frac{1}{2}$f(x),当x∈[0,2]时,f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-2x,0≤x<1}\\{{-2}^{1-|x-\frac{3}{2}|,1≤x<2}}\end{array}\right.$,函数g(x)=x3+3x2+m.若对任意s∈[-4,-2),存在t∈[-4,-2),不等式f(s)-g(t)≥0成立,则实数m的取值范围是( )| A. | (-∞,-12] | B. | (-∞,14] | C. | (-∞,-8] | D. | (-∞,$\frac{31}{2}$] |
分析 对任意s∈[-4,-2),存在t∈[-4,-2),不等式f(s)-g(t)≥0成立,等价于:f(s)min≥g(t)min.利用分段函数的性质可得f(s)min,利用导数研究函数的单调性极值与最值可得g(t)min.
解答 解:对任意s∈[-4,-2),存在t∈[-4,-2),不等式f(s)-g(t)≥0成立,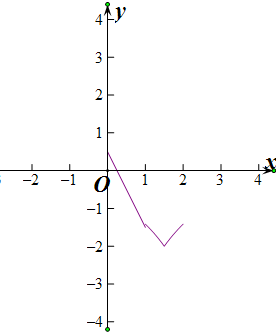
等价于:f(s)min≥g(t)min.
定义在R上的函数f(x)满足f(x+2)=$\frac{1}{2}$f(x),
当x∈[0,2]时,f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-2x,0≤x<1}\\{{-2}^{1-|x-\frac{3}{2}|,1≤x<2}}\end{array}\right.$,
∴x∈[0,2],f(0)=$\frac{1}{2}$为最大值,
∵f(x+2)=$\frac{1}{2}$f(x),
∴f(x)=2f(x+2),
∵x∈[-2,0],
∴f(-2)=2f(0)=2×$\frac{1}{2}$=1,
∵x∈[-4,-2],
∴f(-4)=2f(-2)=2×1=2,
∵?s∈[-4,2),
∴f(s)大=2,
∵f(x)=2f(x+2),
x∈[-2,0],
∴f(-$\frac{1}{2}$)=2f( $\frac{3}{2}$)=2×(-2)=-4,
∵x∈[-4,-3],
∴f(-$\frac{5}{2}$)=2f(-$\frac{1}{2}$)=-8,
∵?s∈[-4,2),
∴f(s)小=-8,
∵函数g(x)=x3+3x2+m,
∴g′(x)=3x2+6x,
3x2+6x>0,x>0,x<-2,
3x2+6x<0,-2<x<0,
3x2+6x=0,x=0,x=-2,
∴函数g(x)=x3+3x2+m,在(-∞,-2)(0,+∞)单调递增.
在(-2,0)单调递减,
∴?t∈[-4,-2),g(t)大=g(-2)=4+m,
g(t)小=g(-4)=m-16,
∵不等式f(s)-g(t)≥0,
∴-8≥m-16,
故实数满足:m≤8,
故选:C.
点评 本题考查了分段函数的性质、利用导数研究函数的单调性极值与最值、等价转化方法,考查了推理能力与计算能力,属于难题.

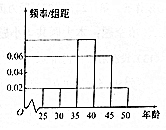 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
(2)现要从年龄低于40岁的员工中用分层抽样的方法抽取42人,则年龄在第1、2、3组的员工人数分别是多少?
(3)为了估计该单位员工的阅读习惯,对第1、2、3组中抽出的42人是否喜欢阅读国学类书籍进行了调查,调查结果如表所示:(单位:人)
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 14 | 22 |
| 合计 | 24 | 18 | 42 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
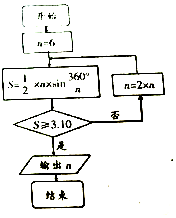 如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )
如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )