题目内容
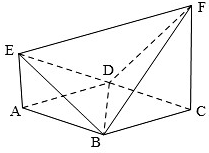 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;(1)证明:平面EAB⊥平面EAD;
(2)求四面体BDEF的体积;
(3)求点B到平面DEF的距离.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,点、线、面间的距离计算
专题:综合题,空间位置关系与距离
分析:(1)证明AB⊥平面EAD,即可证明平面EAB⊥平面EAD;
(2)利用四面体BDEF的体积V=VABCDEF-VE-ABD-VF-BCD=2VB-ACFE-VE-ABD-VF-BCD,即可证明结论;
(3)由余弦定理知cos∠EDF=
=
,所以sin∠EDF=
,求出△DEF的面积,利用等体积,即可求点B到平面DEF的距离.
(2)利用四面体BDEF的体积V=VABCDEF-VE-ABD-VF-BCD=2VB-ACFE-VE-ABD-VF-BCD,即可证明结论;
(3)由余弦定理知cos∠EDF=
| 5+8-9 | ||||
2•
|
| 1 | ||
|
| 3 | ||
|
解答:
(1)证明:由已知:AB⊥EA,AB⊥DA,所以AB⊥平面EAD,
而AB⊆平面EAB,所以平面EAB⊥平面EAD;
(2)解:四面体BDEF的体积V=VABCDEF-VE-ABD-VF-BCD=2VB-ACFE-VE-ABD-VF-BCD
所以四面体BDEF的体积为2
(3)解:先求△DEF的三条边长:DE=
=
,DF=
=2
,
在直角梯形ACFE中,EF=3,
由余弦定理知cos∠EDF=
=
,所以sin∠EDF=
,S△DEF=
•DE•DF•sin∠EDF=
×
×2
×
=3;
设点B到平面DEF的距离为h,由体积法知:VBDEF=
S△DEF•h=
×3×h=2,解出h=2
所以点B到平面DEF的距离为2.
而AB⊆平面EAB,所以平面EAB⊥平面EAD;
(2)解:四面体BDEF的体积V=VABCDEF-VE-ABD-VF-BCD=2VB-ACFE-VE-ABD-VF-BCD
|
所以四面体BDEF的体积为2
(3)解:先求△DEF的三条边长:DE=
| EA2+AD2 |
| 5 |
| FC2+CD2 |
| 2 |
在直角梯形ACFE中,EF=3,
由余弦定理知cos∠EDF=
| 5+8-9 | ||||
2•
|
| 1 | ||
|
| 3 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 | ||
|
设点B到平面DEF的距离为h,由体积法知:VBDEF=
| 1 |
| 3 |
| 1 |
| 3 |
所以点B到平面DEF的距离为2.
点评:本题考查平面与平面垂直的判定,考查体积的计算,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
直线l:y=k(x+1)与圆:x2+4x+y2-5=0在第一象限内部分的图象有交点,k的取值范围( )
A、0≤k≤
| ||
B、-
| ||
C、0<k<
| ||
| D、0<k<5 |
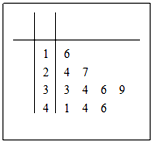 如图是一名篮球运动员在某一赛季10场比赛的得分的原始记录的径叶图,
如图是一名篮球运动员在某一赛季10场比赛的得分的原始记录的径叶图,