题目内容
已知函数y=f(x)的定义域为(0,+∞),满足f(a•b)=f(a)+f(b),且对任意x>1,都有f(x)>0.
(1)求证:f(
)=-f(x);
(2)求证:f(
)=f(a)-f(b);
(3)求证:函数y=f(x)在(0,+∞)上为增函数;
(4)若f(4)=1,解不等式f(2x+1)-f(1-x)>
.
(1)求证:f(
| 1 |
| x |
(2)求证:f(
| a |
| b |
(3)求证:函数y=f(x)在(0,+∞)上为增函数;
(4)若f(4)=1,解不等式f(2x+1)-f(1-x)>
| 1 |
| 2 |
考点:抽象函数及其应用
专题:综合题,函数的性质及应用
分析:(1)令a=b=1,代入得:f(1)=0;令a=
,b=x,可得结论;
(2)f(a)=f(
•b)=f(
)+f(b),可得结论;
(3)利用单调性的定义证明即可;
(4)不等式f(2x+1)-f(1-x)>
,等价于2x+1>2(1-x)>0.
| 1 |
| x |
(2)f(a)=f(
| a |
| b |
| a |
| b |
(3)利用单调性的定义证明即可;
(4)不等式f(2x+1)-f(1-x)>
| 1 |
| 2 |
解答:
(1)证明:∵对任意的a,b∈(0,+∞)都有f(a•b)=f(a)+f(b),
∴令a=b=1,代入得:f(1)=0,
令a=
,b=x,则f(1)=f(
)+f(x)=0,
∴f(
)=-f(x);
(2)证明:∵f(a)=f(
•b)=f(
)+f(b),
∴f(
)=f(a)-f(b);
(3)证明:令0<x1<x2,则
>1,
∵对任意x>1,都有f(x)>0,
∴f(
)>0,
∴f(x2)-f(x1)>0,
∴f(x1)<f(x2),f(x)在(0,+∞)上为增函数;
(4)解:f(4)=1=f(2)+f(2),∴f(2)=
.
∵f(2x+1)-f(1-x)>
.
∴2x+1>2(1-x)>0,
∴
<x<1,即不等式的解集为{x|
<x<1}.
∴令a=b=1,代入得:f(1)=0,
令a=
| 1 |
| x |
| 1 |
| x |
∴f(
| 1 |
| x |
(2)证明:∵f(a)=f(
| a |
| b |
| a |
| b |
∴f(
| a |
| b |
(3)证明:令0<x1<x2,则
| x2 |
| x1 |
∵对任意x>1,都有f(x)>0,
∴f(
| x2 |
| x1 |
∴f(x2)-f(x1)>0,
∴f(x1)<f(x2),f(x)在(0,+∞)上为增函数;
(4)解:f(4)=1=f(2)+f(2),∴f(2)=
| 1 |
| 2 |
∵f(2x+1)-f(1-x)>
| 1 |
| 2 |
∴2x+1>2(1-x)>0,
∴
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查抽象函数及其应用,着重考查赋值法及转化与运算能力,属于中档题.

练习册系列答案
相关题目
函数y=sin(
-2x)的单调递减区间是( )
| π |
| 3 |
A、[-kπ+
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[kπ-
|
函数f(x)=
定义域为( )
| log0.5(x-4) |
| A、[5,+∞) |
| B、(-∞,5] |
| C、(4,5] |
| D、(4,+∞) |
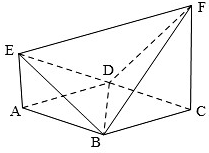 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;