题目内容
直线l:y=k(x+1)与圆:x2+4x+y2-5=0在第一象限内部分的图象有交点,k的取值范围( )
A、0≤k≤
| ||
B、-
| ||
C、0<k<
| ||
| D、0<k<5 |
考点:直线与圆的位置关系
专题:直线与圆
分析:求得圆和x、y轴的正半轴的交点分别为M(1,0)、N(0,
).又直线l:y=k(x+1)经过定点A(-1,0),再求出KAM 和 KAN 的值,可得当直线和圆在第一象限内有交点时,直线的斜率k满足的条件.
| 5 |
解答:
解:圆:x2+4x+y2-5=0即 (x+2)2+y2=9,表示以(-2,0)为圆心,半径等于3的圆.
显然圆和x、y轴的正半轴的交点分别为M(1,0)、N(0,
).
又直线l:y=k(x+1)经过定点A(-1,0),
KAM=0,KAN=
=
,故当直线和圆在第一象限内有交点时,
直线的斜率k满足 0<k<
,
故选:C.
显然圆和x、y轴的正半轴的交点分别为M(1,0)、N(0,
| 5 |
又直线l:y=k(x+1)经过定点A(-1,0),
KAM=0,KAN=
| ||
| 0-(-1) |
| 5 |
直线的斜率k满足 0<k<
| 5 |
故选:C.
点评:本题主要考查圆的标准方程,直线和圆的位置关系、直线的斜率公式,属于基础题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
设a,b∈R,则a<b是(a-b)a2<0的( )
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、既不充分也不必要条件 |
函数y=sin(
-2x)的单调递减区间是( )
| π |
| 3 |
A、[-kπ+
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[kπ-
|
要使sinα-
cosα=
有意义,则m的取值范围是( )
| 3 |
| 4m-6 |
| 4-m |
A、m≤
| ||
| B、m≥-1 | ||
C、-1≤m≤
| ||
D、m≤-1或 m≥
|
已知等比数列{an}中,a4+a6=
dx,则a6(a2+2a4+a6)的值为( )
| ∫ | 2 0 |
| 4-x2 |
| A、π2 | B、4 |
| C、π | D、-9π |
函数f(x)=sin(2x+
)(x∈R)的最小正周期为( )
| π |
| 3 |
A、
| ||
| B、4π | ||
| C、2π | ||
| D、π |
函数f(x)=
定义域为( )
| log0.5(x-4) |
| A、[5,+∞) |
| B、(-∞,5] |
| C、(4,5] |
| D、(4,+∞) |
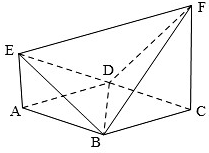 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;