题目内容
设z1是虚数，z2=z1+
是实数，且-1≤z2≤1，求|z1|的值以及z1实部的取值范围．
| 1 |
| z1 |
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：设z1=a+bi，a，b∈R且b≠0，可得z2，由实数可得a，b的式子，可得|z1|的值和a的范围．
解答：
解：设z1=a+bi，a，b∈R且b≠0，
则z2=z1+
=a+bi+
=(a+
)+(b-
)i
∵z2是实数，b≠0，于是有a2+b2=1，即|z1|=1，还可得z2=2a
由-1≤z2≤1，得-1≤2a≤1，解得-
≤a≤
，
∴z1的实部的取值范围是[-
，
]．
则z2=z1+
| 1 |
| z1 |
| 1 |
| a+bi |
| a |
| a2+b2 |
| b |
| a2+b2 |
∵z2是实数，b≠0，于是有a2+b2=1，即|z1|=1，还可得z2=2a
由-1≤z2≤1，得-1≤2a≤1，解得-
| 1 |
| 2 |
| 1 |
| 2 |
∴z1的实部的取值范围是[-
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题考查复数的代数形式的混合运算，属基础题．
练习册系列答案
相关题目
函数f（x）=sin（2x+
）（x∈R）的最小正周期为（ ）
| π |
| 3 |
A、
| ||
| B、4π | ||
| C、2π | ||
| D、π |
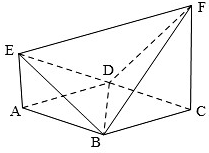如图，已知ABCD是边长为2的正方形，EA⊥平面ABCD，FC⊥平面ABCD，设EA=1，FC=2；
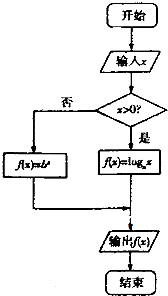在如图所示的程序框图中，当输入实数x的值为4时，输出的结果为2；当输入实数x的值为-2时，输出的结果为4．