题目内容
从A、B、C三个男生和D、E两个女生中,每次随机抽取1人,连续抽取2次.
(1)若采用不放回抽取,求取出的2人不全是男生的概率;
(2)若采用有放回抽取,求:
①2次抽到同一人的概率;
②抽取的2人不全是男生的概率.
(1)若采用不放回抽取,求取出的2人不全是男生的概率;
(2)若采用有放回抽取,求:
①2次抽到同一人的概率;
②抽取的2人不全是男生的概率.
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)先计算从三个男生和两个女生中,连续不放回抽取2次的抽法总数及取出的2人不全是男生的抽法次数,代入古典概型概率计算公式,可得答案.
(2)先计算从三个男生和两个女生中,有放回抽取2次的抽法总数,
①再计算2次抽到同一人的抽法次数,代入古典概型概率计算公式,可得答案.
②再计算取出的2人不全是男生的抽法次数,代入古典概型概率计算公式,可得答案.
(2)先计算从三个男生和两个女生中,有放回抽取2次的抽法总数,
①再计算2次抽到同一人的抽法次数,代入古典概型概率计算公式,可得答案.
②再计算取出的2人不全是男生的抽法次数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)若采用不放回抽取,则从三个男生和两个女生中,连续抽取2次,
共有
=10种抽取方法,
其中取出的2人不全是男生有:
+
•
=1+6=7种,
∴取出的2人不全是男生的概率P=
,
(2)若采用有放回抽取,则有
•
=25种抽取方法:
①其中2次抽到同一人的抽法有:
•
=5,
故2次抽到同一人的概率P=
=
;
②抽取的2人不全是男生有:
•
+
•
+
•
=16种,
故抽取的2人不全是男生的概率P=
.
共有
| C | 2 5 |
其中取出的2人不全是男生有:
| C | 2 2 |
| C | 1 3 |
| C | 1 2 |
∴取出的2人不全是男生的概率P=
| 7 |
| 10 |
(2)若采用有放回抽取,则有
| C | 1 5 |
| C | 1 5 |
①其中2次抽到同一人的抽法有:
| C | 1 5 |
| C | 1 1 |
故2次抽到同一人的概率P=
| 5 |
| 25 |
| 1 |
| 5 |
②抽取的2人不全是男生有:
| C | 1 2 |
| C | 1 2 |
| C | 1 3 |
| C | 1 2 |
| C | 1 2 |
| C | 1 3 |
故抽取的2人不全是男生的概率P=
| 16 |
| 25 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
设a,b∈R,则a<b是(a-b)a2<0的( )
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、既不充分也不必要条件 |
函数f(x)=sin(2x+
)(x∈R)的最小正周期为( )
| π |
| 3 |
A、
| ||
| B、4π | ||
| C、2π | ||
| D、π |
函数f(x)=
定义域为( )
| log0.5(x-4) |
| A、[5,+∞) |
| B、(-∞,5] |
| C、(4,5] |
| D、(4,+∞) |
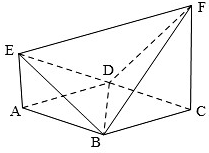 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;