题目内容
已知|
|=3，|
|=6，
与
的夹角为θ，
（1）若
∥
，求
•
；
（2）若（
-
）⊥
，求θ．
| a |
| b |
| a |
| b |
（1）若
| a |
| b |
| a |
| b |
（2）若（
| a |
| b |
| a |
考点：数量积表示两个向量的夹角,平面向量数量积的运算,数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：（1）当
∥
时，夹角为θ=0°或180°，由数量积的定义可得；（2）由垂直可得（
-
）•
=0，可得cosθ的方程，解方程可得cosθ，可得θ．
| a |
| b |
| a |
| b |
| a |
解答：
解：（1）|
|=3，|
|=6，
与
的夹角为θ
当
∥
时，夹角为θ=0°或180°，
∴
•
=|
||
|cosθ=±18；
（2）∵（
-
）⊥
，∴（
-
）•
=0，
∴
2-
•
=9-3×6×cosθ=0，
解得cosθ=
，∴θ=60°
| a |
| b |
| a |
| b |
当
| a |
| b |
∴
| a |
| b |
| a |
| b |
（2）∵（
| a |
| b |
| a |
| a |
| b |
| a |
∴
| a |
| a |
| b |
解得cosθ=
| 1 |
| 2 |
点评：本题考查平面向量的夹角公式，涉及向量的平行和垂直，属中档题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
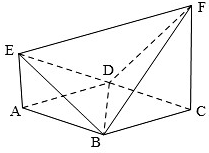如图，已知ABCD是边长为2的正方形，EA⊥平面ABCD，FC⊥平面ABCD，设EA=1，FC=2；
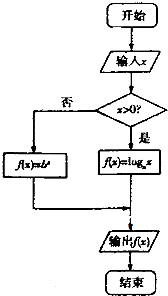在如图所示的程序框图中，当输入实数x的值为4时，输出的结果为2；当输入实数x的值为-2时，输出的结果为4．