题目内容
在面积为S的△ABC的边上AC任取一点P1,“使P1BC的面积大于
”的概率等于( )
| S |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:本题是几何概型问题,欲求△P1BC的面积大于
的概率,转化为在边AC上使得CD的长度大于
的概率,先由在边AC上使得CP的长度大于
的线段的长度为
AC,根据几何概型概率公式解答.
| S |
| 3 |
| AC |
| 3 |
| AC |
| 3 |
| 2 |
| 3 |
解答:
解:本题是几何概型问题,测度为线段的长度.
“△P1BC的面积大于
的概率”事件对应的区域长度为AP=
AC,如图

则△P1BC的面积大于
的概率是
=
.
故选C.
“△P1BC的面积大于
| S |
| 3 |
| 2 |
| 3 |

则△P1BC的面积大于
| S |
| 3 |
| ||
| AC |
| 2 |
| 3 |
故选C.
点评:本小题主要考查几何概型、几何概型的应用、三角形的面积等基础知识,考查化归与转化思想.属于基础题.一般地,在几何区域D中随机地取一点,记事件“该点落在其内部一个区域d内”为事件A,则事件A发生的概率为:
P(A)=
.
P(A)=
| 构成事件A的区域长度(面积或者体积) |
| 实验的全部结果构成的区域长度(面积或者体积) |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知|
|=1,
与
夹角为
,|2
+
|=
,则|
|等于( )
| a |
| a |
| b |
| 2π |
| 3 |
| a |
| b |
| 7 |
| b |
| A、1 | B、2 | C、3 | D、4 |
已知两个非零向量
=(m-1,n-1)和
(m-3,n-3),若cos<
,
>≤0,则m+n的取值范围是( )
| a |
| b |
| a |
| b |
A、[
| ||||
| B、[2,6] | ||||
C、(
| ||||
| D、(2,6) |
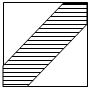 在边长为25cm的正方形中挖去腰长为23cm的两个等腰直角三角形(如图),现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是
在边长为25cm的正方形中挖去腰长为23cm的两个等腰直角三角形(如图),现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是