题目内容

13．复数z=$\frac{3+i}{1-i}$（其中i为虚数单位）对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 直接利用复数的除法的运算法则化简求解即可．

解答 解：复数z=$\frac{3+i}{1-i}$=$\frac{（3+i）（1+i）}{（1-i）（1+i）}$=$\frac{2+4i}{2}$=1+2i．
复数对应点（1，2）在第一象限．
故选：A．

点评 本题考查复数代数形式混合运算，考查计算能力．

练习册系列答案
相关题目
11．已知函数f（x）=x2-2tx+2在[0，1]的最小值为g（t），则g（t）的表达式为g（t）=$\left\{\begin{array}{l}{2，}&{t≤0}\\{-{t}^{2}+2，}&{0＜t＜1}\\{-2t+3，}&{t≥1}\end{array}\right.$．
4．设变量x，y满足约束条件$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10＜0\\ x+y-8≤0\end{array}\right.$，则目标函数z=3x-4y的取值范围是（　　）
A．[-11，3）B．[-11，3]C．（-11，3）D．（-11，3]
1．弹簧振子的振动在简谐振动，如表给出的振子在完成一次全振动的过程中的时间t与位移y之间的对应数据，根据这些数据求出这个振子的振动的函数解析式为y=-20cos（$\frac{π}{6{t}_{0}}$t）．
t0t02t03t04t05t06t07t08t09t010t011t012t0
 y-20.0-17.8-10.1 0.1 10.3 17.1 20.0 17.7 10.3 0.1-10.1-17.8-20.0 
8．已知函数$f（x）=\sqrt{3}sinxcosx+{sin^2}x-\frac{1}{2}$．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求f（x）在区间$[\frac{π}{4}，\frac{π}{2}]$上的最大值和最小值．
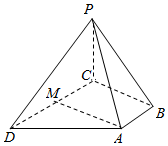18．如图：四棱锥P-ABCD中，PD=PC，底面ABCD是直角梯形AB⊥BC，AB∥CD，CD=2AB，点M是CD的中点．
（1）求证：AM∥平面PBC；
（2）求证：CD⊥PA．
5．已知数列{an}的前n项和为Sn，且a1=1，Sn=Sn-1+an-1+2n-2（n≥2）
（1）求数列{an}的通项公式；
（2）设bn=（2n-1）an+1，记f（n）=b1+b2+…+bn，若 对任意n，（n∈N*），不等式f（n）＜λ•an+1成立，求实数λ的取值范围．
2．已知非零平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，“|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
3．已知|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，$\overrightarrow a$与$\overrightarrow b$的夹角为120°，$\overrightarrow c$=$\overrightarrow a$+2$\overrightarrow b$，$\overrightarrow d$=2$\overrightarrow a$+k$\overrightarrow b$，当实数k取何值时：
（1）$\overrightarrow c⊥\overrightarrow d$．
（2）$\overrightarrow c∥\overrightarrow d$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网