题目内容
已知f(x)为R上的奇函数,当x>0时,f(x)=3x,那么f(log
4)的值为 .
| 1 |
| 2 |
考点:函数奇偶性的性质
专题:计算题
分析:要求f(log
4)的值,即求f(-2)的值,可通过奇函数的定义转换为求f(2),而条件中给出了x>0的表达式,代入即可,问题解决.
| 1 |
| 2 |
解答:
解:因为f(x)为R上的奇函数,所以f(-x)=-f(x),
又因为log
4=-log24=-2<0,所以f(log
4)=f(-2)=-f(2)
又当x>0时,f(x)=3x,所以f(2)=9,f(-2)=-9.
故答案为:-9.
又因为log
| 1 |
| 2 |
| 1 |
| 2 |
又当x>0时,f(x)=3x,所以f(2)=9,f(-2)=-9.
故答案为:-9.
点评:本题是函数奇偶性的一个应用:求函数值的运算.通常要把负的函数值转化为正的来求,注意运用奇偶函数的定义,有时也可先求出x<0的表达式,代入即得.本题属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知角α的终边和单位圆的交点为P,则点P的坐标为( )
| A、(sinα,cosα) |
| B、(cosα,sinα) |
| C、(sinα,tanα) |
| D、(tanα,sinα) |
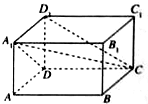 在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.
在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.