题目内容
12.已知函数f(x)=3sin(ωx+φ),g(x)=3cos(ωx+φ),若对任意x∈R,都有f($\frac{π}{6}$+x)=f($\frac{π}{6}$-x),则g($\frac{π}{6}$)=0.分析 由题意可得f(x)的图象关于直线x=$\frac{π}{6}$对称,故有ω•$\frac{π}{6}$+φ=kπ+$\frac{π}{2}$,k∈Z,由此求得g($\frac{π}{6}$)=3cos(ω•$\frac{π}{6}$+φ)的值.
解答 解:根据f($\frac{π}{6}$+x)=f($\frac{π}{6}$-x),可得f(x)的图象关于直线x=$\frac{π}{6}$对称,
∴ω•$\frac{π}{6}$+φ=kπ+$\frac{π}{2}$,k∈Z,∴g($\frac{π}{6}$)=3cos(ω•$\frac{π}{6}$+φ)=0,
故答案为:0.
点评 本题主要考查正弦函数的图象的对称性,求三角函数的值,属于基础题.

练习册系列答案
相关题目
10.已知命题p:?x∈R,sinx≤1,则¬p为( )
| A. | ?x∈R,sinx≤1 | B. | ?x∈R,sinx>1 | C. | ?x∈R,sinx≥1 | D. | ?x∈R,sinx>1 |
11.若双曲线$\frac{x^2}{3}-{y^2}=1$的左焦点在抛物线y2=2px的准线上,则p的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $4\sqrt{2}$ |
8.已知点A($\sqrt{3}$,0)和P($\sqrt{3}$,t)(t∈R).若曲线x=$\sqrt{3-{y}^{2}}$上存在点B使∠APB=60°,则t的取值范围是( )
| A. | (0,1+$\sqrt{3}$] | B. | [0,1+$\sqrt{3}$] | C. | [-1-$\sqrt{3}$,1+$\sqrt{3}$] | D. | [-1-$\sqrt{3}$,0)∪(0,1+$\sqrt{3}$] |
1.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间为( )
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$]k∈Z | B. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$]k∈Z | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$]k∈Z | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$]k∈Z |
2.“若x2=1,则x=1”的否命题为( )
| A. | 若x2≠1,则x=1 | B. | 若x2=1,则x≠1 | C. | 若x2≠1,则x≠1 | D. | 若x≠1,则x2≠1 |
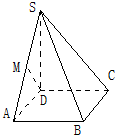 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.