题目内容
2.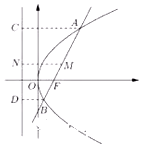 已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.
已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.(1)求直线FN与直线AB的夹角θ的大小;
(2)求证:点B、O、C三点共线.
分析 (1)先设A(x1,y1)、B(x2,y2)、中点M(x0,y0),利用斜率公式得出kFN=-$\frac{1}{2}$y0,再分类讨论:当x1=x2时,显然FN⊥AB;当x1≠x2时,证出kFN•kAB=-1.从而知FN⊥AB成立,即可得出结论.
(2)将焦点弦AB的直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合直线斜率的关系即可证得B、O、C三点共线,从而解决问题.
解答 (1)解:设A(x1,y1)、B(x2,y2)、中点M(x0,y0),焦点F的坐标是(1,0).
kFN=-$\frac{1}{2}$y0,当x1=x2时,显然FN⊥AB;
当x1≠x2时,kAB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{2}{{y}_{0}}$,
∴kFN•kAB=-1.
∴FN⊥AB.综上所述知FN⊥AB成立,
即直线FN与直线AB的夹角θ的大小为90°;
(2)证明:由y=k(x-1)与抛物线方程联立,可得ky2-4y-4k=0,∴y1y2=-4,
∴A在准线上的射影为C,
∴C(-1,y1),∴kOC=-y1,
∵kOB=$\frac{{y}_{2}}{{x}_{2}}$=$\frac{4}{{y}_{2}}$,y1y2=-4,
∴kOB=kOC,∴点B、O、C三点共线.
点评 本题给出抛物线过焦点的弦在准线上的射影,求证三点共线及线线角,着重考查了用解析几何理解抛物线的定义的知识点,属于中档题.

练习册系列答案
相关题目
7.在(x-$\frac{1}{x}$)10的二项展开式中,x4的系数等于( )
| A. | -120 | B. | -60 | C. | 60 | D. | 120 |
12.设a=2ln$\frac{3}{2}$、b=log2$\frac{1}{3}$、c=($\frac{1}{2}$)-0.3,则( )
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | b<a<c |
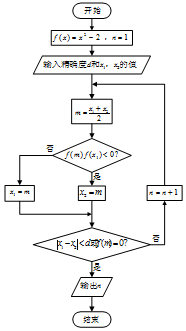 二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )