题目内容
12.设f(x)=|x+1|-|x-4|.(1)若f(x)≤-m2+6m恒成立,求实数m的取值范围;
(2)设m的最大值为m0,a,b,c均为正实数,当3a+4b+5c=m0时,求a2+b2+c2的最小值.
分析 (1)求出f(x)=|x+1|-|x-4|的最大值,f(x)max≤-m2+6m即可.
(2)由柯西不等式(a2+b2+c2)(32+42+52)≥(3a+4b+5c)2=25
解答 解(1)-5≤|x+1|-|x-4|≤5.,
由于f(x)≤-m2+6m的解集为R,
∴-m2+6m≥5,即1≤m≤5.
(2)由(1)得m的最大值为5,∴3a+4b+5c=5
由柯西不等式(a2+b2+c2)(32+42+52)≥(3a+4b+5c)2=25----------(5分)
故a2+b2+c2≥$\frac{1}{2}$.(当且仅当a=$\frac{3}{10}$,b=$\frac{4}{10}$c=$\frac{5}{10}$时取等号)
∴a2+b2+c2的最小值为$\frac{1}{2}$.
点评 本题考查绝对值不等式的最值,柯西不等式的应用,属于中档题.

练习册系列答案
相关题目
2.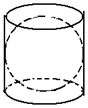 如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
 如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )| A. | 2R | B. | $\frac{4R}{3}$ | C. | $\frac{2}{3}R$ | D. | $\frac{R}{3}$ |
17.如图为某几何体的三视图,则其体积为( )
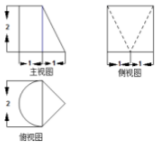

| A. | π+$\frac{4}{3}$ | B. | $\frac{π}{3}$+4 | C. | $\frac{2}{3}$π+$\frac{4}{3}$ | D. | $\frac{2}{3}$π+4 |
4.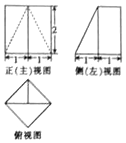 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{32}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
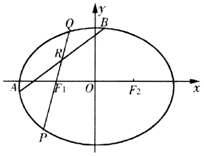 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点. 已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.
已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.