题目内容
已知函数f(x)=|x-8︳-︳x-4︳
(1)解不等式f(x)>2;
(2)若f(x)>
t2-4t+2恒成立,求实数t的取值范围.
(1)解不等式f(x)>2;
(2)若f(x)>
| 1 |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)函数f(x)=
,令-2x+12=2,求得x=5,可得不等式f(x)>2的解集.
(2)由(1)可得,-4≤f(x)≤4,要使f(x)>
t2-4t+2恒成立,只要-4>
t2-4t+2,解此一元二次不等式求得t的范围.
|
(2)由(1)可得,-4≤f(x)≤4,要使f(x)>
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)函数f(x)=|x-8︳-︳x-4︳=
,令-2x+12=2,求得x=5,
故不等式f(x)>2的解集为(-∞,5).
(2)由(1)可得,-4≤f(x)≤4,要使f(x)>
t2-4t+2恒成立,只要-4>
t2-4t+2,
即t2-8t+12<0,求得2<t<6.
|
故不等式f(x)>2的解集为(-∞,5).
(2)由(1)可得,-4≤f(x)≤4,要使f(x)>
| 1 |
| 2 |
| 1 |
| 2 |
即t2-8t+12<0,求得2<t<6.
点评:本题主要考查带有绝对值的函数,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知f(x)=(x+1)(x+a)为偶函数,则a=( )
| A、-2 | B、-1 | C、1 | D、2 |
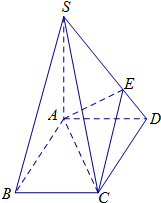 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.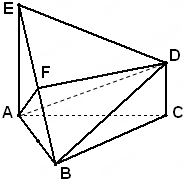 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: