题目内容
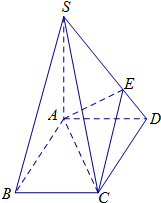 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.(Ⅰ)当SD⊥平面AEC时,求
| SE |
| DE |
(Ⅱ)当二面角E-AC-D的余弦值为
2
| ||
| 5 |
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间角
分析:(Ⅰ)当SD⊥平面AEC时,判断SD与AE的关系,通过解三角形即可求
的值;
(Ⅱ)确定,∴∠EAD就是二面角E-AC-D的平面角,利用(Ⅰ)的数据关系,推出当二面角E-AC-D的余弦值为
时,直线CD与平面ACE所成角的具体位置,然后求直线CD与平面ACE所成角的正弦值.
| SE |
| DE |
(Ⅱ)确定,∴∠EAD就是二面角E-AC-D的平面角,利用(Ⅰ)的数据关系,推出当二面角E-AC-D的余弦值为
2
| ||
| 5 |
解答:
解:(Ⅰ)当SD⊥平面AEC时,可得SD⊥AE,SA⊥底面ABCD,SA=AB=2,AD=1,
∴SA⊥AD,∴SD=
,AE=
,
=
=
=4.
(Ⅱ)底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,
∴AC⊥AD,SA⊥AC,AS∩AD=A,∴AC⊥平面SAD,
∴∠EAD就是二面角E-AC-D的平面角,
由(Ⅰ)可知:SD⊥平面AEC时,AE=
,此时二面角E-AC-D的余弦值为
,直线CD与平面ACE所成的角就是∠ECD,
它的正弦值为:
=
=
=
.

∴SA⊥AD,∴SD=
| 5 |
| 2 | ||
|
| SE |
| DE |
| ||
|
| ||||
|
(Ⅱ)底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,
∴AC⊥AD,SA⊥AC,AS∩AD=A,∴AC⊥平面SAD,
∴∠EAD就是二面角E-AC-D的平面角,
由(Ⅰ)可知:SD⊥平面AEC时,AE=
| 2 | ||
|
2
| ||
| 5 |
它的正弦值为:
| ED |
| CD |
| ||
| CD |
| ||||
| 2 |
| ||
| 10 |
点评:本题考查张筱雨平面所成角的求法,二面角的应用,直线与平面垂直的判定定理的应用,考查转化思想以及计算能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知z=
,则z的共轭复数为( )
| 5i |
| 1-2i |
| A、2-i | B、2+i |
| C、-2-i | D、-2+i |
直三棱柱ABC-EFG所有顶点在半径为
的球面上,AB=AC=
,AE=2,B-AE-C余弦为( )
| 2 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列推理正确的是( )
| A、把a(b+c)与loga(x+y)类比,则有loga(x+y)=logax+logay |
| B、把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny |
| C、把a(b+c)与ax+y类比,则有ax+y=ax+ay |
| D、把a(b+c)与a*(b+c)类比,则有a*(b+c)=a*b+a* |
在几何体P-ABCD中,ABCD为矩形,各棱所在直线共有异面直线( )


| A、4对 |
| B、6对 |
| C、8对 |
| D、12对 ( |
