题目内容
A、B、C为△ABC内角,R为△ABC外接圆半径,r为△ABC内切圆半径.
(1)求证:tanA+tanB+tanC=tanAtanBtanC(A,B,C≠
);
(2)求证:2Rr=
.
(1)求证:tanA+tanB+tanC=tanAtanBtanC(A,B,C≠
| π |
| 2 |
(2)求证:2Rr=
| abc |
| a+b+c |
考点:两角和与差的正切函数,三角形的面积公式
专题:三角函数的求值
分析:(1)根据内角和定理得A+B=π-C,代入两角和的正切公式化简即可;
(2)利用等面积法列出等式,再由
=2R得到sinC,代入化简即可.
(2)利用等面积法列出等式,再由
| c |
| sinC |
解答:
证明:(1)由A+B+C=π,得A+B=π-C,
则tan(A+B)=-tanC=
,
化简得,tanA+tanB+tanC=tanAtanBtanC;
(2)由题意得,r为△ABC内切圆半径
则S△ABC=
absinC=
r(a+b+c),
又
=2R,得sinC=
,代入上式得
ab
=
r(a+b+c),
化简得,2Rr=
.
则tan(A+B)=-tanC=
| tanA+tanB |
| 1-tanAtanB |
化简得,tanA+tanB+tanC=tanAtanBtanC;
(2)由题意得,r为△ABC内切圆半径
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又
| c |
| sinC |
| c |
| 2R |
| 1 |
| 2 |
| c |
| 2R |
| 1 |
| 2 |
化简得,2Rr=
| abc |
| a+b+c |
点评:本题考查两角和的正切公式,内角和定理,以及等面积法的应用,属于中档题.

练习册系列答案
相关题目
36°化为弧度制为( )
A、
| ||
B、
| ||
| C、5 | ||
| D、5π |
如图所示的程序框图,它的输出结果是( )


| A、3 | B、4 | C、5 | D、6 |
设向量
=(2,3),
=(-1,2),若m
+
与
-2
平行,则实数m等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|

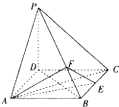 如图,ABCD是正方形,PD⊥平面ABCD,点E是BC中点,点F在PB上,且PE=2FB.
如图,ABCD是正方形,PD⊥平面ABCD,点E是BC中点,点F在PB上,且PE=2FB. 已知函数f(x)=-2
已知函数f(x)=-2