题目内容
复数m2-1+(m+1)i是纯虚数,则实数m的值为( )
| A、-1 | B、1 | C、±1 | D、±2 |
考点:复数的基本概念
专题:数系的扩充和复数
分析:根据复数纯虚数的概念进行求解即可.
解答:
解:若复数m2-1+(m+1)i是纯虚数,
则m2-1=0且m+1≠0,
解得m=±1且m≠-1,
解得m=1,
故选:B
则m2-1=0且m+1≠0,
解得m=±1且m≠-1,
解得m=1,
故选:B
点评:本题主要考查复数的有关概念的应用,比较基础.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
在复平面内,复数z=
对应的点位于( )
| 2i |
| -1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数y=sin(
-2x),x∈R是( )
| π |
| 2 |
| A、最小正周期为π的奇函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的偶函数 | ||
D、最小正周期为
|
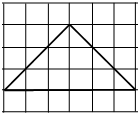
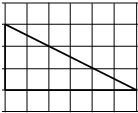
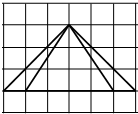
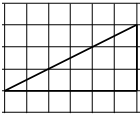
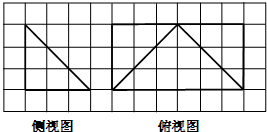 如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )
如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )